Các dạng toán phép tịnh tiến

Bài viết trình bày lý thuyết và các dạng toán phép tịnh tiến trong chương trình Hình học 11 chương 1. Kiến thức và các ví dụ trong bài viết được tham khảo từ các tài liệu phép dời hình và phép đồng dạng trong mặt phẳng được chia sẻ trên TOANMATH.com.

A. KIẾN THỨC CẦN NẮM
1. Định nghĩa phép tịnh tiến
• Trong mặt phẳng cho vectơ $\vec{v}$ . Phép biến hình biến mỗi điểm $M$ thành điểm $M^{'}$ sao cho $\vec{M M^{'}} = \vec{v}$ được gọi là phép tịnh tiến theo vectơ $\vec{v}$ , ký hiệu $T_{\vec{v}} .$
• $T_{\vec{v}} (M) = M^{'}$ $\Leftrightarrow \vec{M M^{'}} = \vec{v} .$
2. Biểu thức tọa độ của phép tịnh tiến:Trong mặt phẳng tọa độ $O x y$ , cho điểm $M (x; y)$ và $\vec{v} = (a; b) .$ Khi đó: $M^{'} (x^{'}; y^{'}) = T_{\vec{v}} (M)$ $\Leftrightarrow \vec{M M^{'}} = \vec{v}$ $\Leftrightarrow {\begin{cases} x^{'} - x = a \\ y^{'} - y = b \end{cases}$ $\Leftrightarrow {\begin{cases} x^{'} = x + a \\ y^{'} = y + b \end{cases}$
3. Các tính chất của phép tịnh tiến
• Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ.
• Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho.
• Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.
• Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
• Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

B. CÁC DẠNG TOÁN PHÉP TỊNH TIẾN
Dạng toán 1. Xác định ảnh của một hình qua phép tịnh tiến
Phương pháp: Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến.

Ví dụ 1. Cho tam giác $A B C$ , dựng ảnh của tam giác $A B C$ qua phép tịnh tiến theo vectơ $\vec{B C} .$

cac-dang-toan-phep-tinh-tien-1

Ta có: $T_{\vec{B C}} (B) = C .$
Để tìm ảnh của điểm $A$ , ta dựng hình bình hành $A B C D .$
Do $\vec{A D} = \vec{B C}$ nên $T_{\vec{B C}} (A) = D .$
Gọi $E$ là điểm đối xứng với $B$ qua $C$ , khi đó: $\vec{C E} = \vec{B C} .$
Suy ra $T_{\vec{B C}} (C) = E .$
Vậy ảnh của tam giác $A B C$ là tam giác $D C E$ .

Ví dụ 2. Trong mặt phẳng tọa độ $O x y$ , cho $\vec{v} = (- 2; 3)$ . Hãy tìm ảnh của điểm $A (1; - 1)$ qua phép tịnh tiến theo vectơ $\vec{v}$ .

Gọi $A^{'} (x^{'}; y^{'})$ là ảnh của điểm $A$ qua phép tịnh tiến theo vectơ $\vec{v}$ .
Áp dụng biểu thức tọa độ của phép tịnh tiến ${\begin{cases} x^{'} = x + a \\ y^{'} = y + b \end{cases}$
Ta có: $A^{'} (x^{'}; y^{'}) = T_{\vec{v}} (A)$ $\Rightarrow {\begin{cases} x^{'} = 1 + (- 2) \\ y^{'} = - 1 + 3 \end{cases}$ $\Leftrightarrow {\begin{cases} x^{'} = - 1 \\ y^{'} = 2 \end{cases}$ $\Rightarrow A^{'} (- 1; 2) .$

Ví dụ 3. Trong mặt phẳng tọa độ $O x y$ , cho $\vec{v} = (1; - 3)$ và đường thẳng $d$ có phương trình $2 x - 3 y + 5 = 0.$ Viết phương trình đường thẳng $d^{'}$ là ảnh của $d$ qua phép tịnh tiến $T_{\vec{v}} .$

Cách 1.
Lấy điểm $M (x; y)$ tùy ý thuộc $d$ , ta có: $2 x - 3 y + 5 = 0$ $(*) .$
Gọi $M^{'} (x^{'}; y^{'}) = T_{\vec{v}} (M)$ $\Rightarrow {\begin{cases} x^{'} = x + 1 \\ y^{'} = y - 3 \end{cases}$ $\Leftrightarrow {\begin{cases} x = x^{'} - 1 \\ y = y^{'} + 3 \end{cases}$
Thay vào $(*)$ ta được phương trình $2 (x^{'} - 1) - 3 (y^{'} + 3) + 5 = 0$ $\Leftrightarrow 2 x^{'} - 3 y^{'} - 6 = 0.$
Vậy ảnh của $d$ là đường thẳng $d^{'} : 2 x - 3 y - 6 = 0.$
Cách 2.
Do $d^{'} = T_{\vec{v}} (d)$ nên $d^{'}$ song song hoặc trùng với $d$ , vì vậy phương trình đường thẳng $d^{'}$ có dạng $2 x - 3 y + c = 0.$
Lấy điểm $M (- 1; 1) \in d .$ Khi đó $M^{'} = T_{\vec{v}} (M)$ $= (- 1 + 1; 1 - 3) = (0; - 2) .$
Do $M^{'} \in d^{'}$ $\Rightarrow 2.0 - 3. (- 2) + c = 0$ $\Leftrightarrow c = - 6.$
Vậy ảnh của $d$ là đường thẳng: $d^{'} : 2 x - 3 y - 6 = 0.$
Cách 3.
Lấy $M (- 1; 1)$ , $N (2; 3)$ thuộc $d$ , ảnh của $M$ , $N$ qua phép tịnh tiến $T_{\vec{v}}$ tương ứng là $M^{'} (0; - 2)$ , $N^{'} (3; 0) .$
Vì $d^{'}$ đi qua hai điểm $M^{'}, N^{'}$ nên $d^{'}$ có phương trình $\frac{x - 0}{3} = \frac{y + 2}{2}$ $\Leftrightarrow 2 x - 3 y - 6 = 0.$

Ví dụ 4. Trong mặt phẳng tọa độ $O x y$ , cho đường tròn $(C)$ có phương trình $x^{2} + y^{2} + 2 x - 4 y - 4 = 0.$ Tìm ảnh của $(C)$ qua phép tịnh tiến theo vectơ $\vec{v} = (2; - 3) .$

Cách 1.
Lấy điểm $M (x; y)$ tùy ý thuộc đường tròn $(C)$ , ta có: $x^{2} + y^{2} + 2 x - 4 y - 4 = 0$ $(*) .$
Gọi $M^{'} (x^{'}; y^{'}) = T_{\vec{v}} (M)$ $\Rightarrow {\begin{cases} x^{'} = x + 2 \\ y^{'} = y - 3 \end{cases}$ $\Leftrightarrow {\begin{cases} x = x^{'} - 2 \\ y = y^{'} + 3 \end{cases}$
Thay vào phương trình $(*)$ ta được: ${(x^{'} - 2)}^{2} + {(y^{'} + 3)}^{2}$ $+ 2 (x^{'} - 2) - 4 (y^{'} + 3) - 4 = 0$ $\Leftrightarrow x ‘^{2} + y ‘^{2} - 2 x^{'} + 2 y^{'} - 7 = 0.$
Vậy ảnh của $(C)$ là đường tròn $(C^{'})$ : $x^{2} + y^{2} - 2 x + 2 y - 7 = 0.$
Cách 2.
Ta có: $(C)$ có tâm $I (- 1; 2)$ và bán kính $r = 3.$
Gọi $(C^{'}) = T_{\vec{v}} ((C))$ và $I^{'} (x^{'}; y^{'})$ , $r^{'}$ là tâm và bán kính của $(C^{'}) .$
Ta có: ${\begin{cases} x^{'} = - 1 + 2 = 1 \\ y^{'} = 2 - 3 = - 1 \end{cases}$ $\Rightarrow I^{'} (1; - 1)$ và $r^{'} = r = 3$ nên phương trình của đường tròn $(C^{'})$ là: ${(x - 1)}^{2} + {(y + 1)}^{2} = 9.$

Dạng toán 2. Xác định phép tịnh tiến khi biết ảnh và tạo ảnh
Phương pháp: Xác định phép tịnh tiến tức là tìm tọa độ của $\vec{v}$ . Để tìm tọa độ của $\vec{v}$ ta có thể giả sử $\vec{v} = (a; b)$ , sử dụng các dữ kiện trong giả thiết của bài toán để thiết lập hệ phương trình hai ẩn $a, b$ và giải hệ tìm $a, b$ .
[ads]
Ví dụ 5. Trong mặt phẳng tọa độ $O x y$ , cho đường thẳng $d : 3 x + y - 9 = 0$ . Tìm phép tịnh tiến theo vectơ $\vec{v}$ có giá song song với $O y$ biến $d$ thành $d^{'}$ đi qua điểm $A (1; 1)$ .

Vì $\vec{v}$ có giá song song với $O y$ nên $\vec{v} = (0; k)$ $(k \neq 0) .$
Lấy $M (x; y) \in d$ $\Rightarrow 3 x + y - 9 = 0$ $(*) .$
Gọi $M^{'} (x^{'}; y^{'}) = T_{\vec{v}} (M)$ $\Rightarrow {\begin{cases} x^{'} = x \\ y^{'} = y + k \end{cases}$
Thay vào $(*)$ , ta được: $3 x^{'} + y^{'} - k - 9 = 0.$
Do đó: $T_{\vec{v}} (d) = d^{'} :$ $3 x + y - k - 9 = 0.$
Mà: $A (1; 1)$ thuộc $d$ , suy ra: $k = - 5.$
Vậy $\vec{v} = (0; - 5) .$

Ví dụ 6. Trong mặt phẳng tọa độ $O x y$ , cho hai đường thẳng $d : 2 x - 3 y + 3 = 0$ và $d^{'} : 2 x - 3 y - 5 = 0.$ Tìm tọa độ $\vec{v}$ có phương vuông góc với $d$ để $T_{\vec{v}} (d) = d^{'} .$

Đặt $\vec{v} = (a; b) .$
Lấy điểm $M (x; y)$ tùy ý thuộc $d$ , ta có: $d : 2 x - 3 y + 3 = 0$ $(*) .$
Gọi $M^{'} (x^{'}; y^{'}) = T_{\vec{v}} (M) .$ Ta có ${\begin{cases} x^{'} = x + a \\ y^{'} = y + b \end{cases}$ $\Leftrightarrow {\begin{cases} x = x^{'} - a \\ y = y^{'} - b \end{cases}$ , thay vào $(*)$ ta được phương trình: $2 x^{'} - 3 y^{'} - 2 a + 3 b + 3 = 0.$
Từ giả thiết suy ra $- 2 a + 3 b + 3 = - 5$ $\Leftrightarrow 2 a - 3 b = - 8.$
Vectơ pháp tuyến của đường thẳng $d$ là $\vec{n} = (2; - 3)$ , suy ra vectơ chỉ phương của $d$ là $\vec{u} = (3; 2) .$
Do $\vec{v} ⊥ \vec{u}$ $\Rightarrow \vec{v} . \vec{u} = 3 a + 2 b = 0.$
Ta có hệ phương trình ${\begin{cases} 2 a - 3 b = - 8 \\ 3 a + 2 b = 0 \end{cases}$ $\Leftrightarrow {\begin{cases} a = - \frac{16}{13} \\ b = \frac{24}{13} \end{cases}$
Vậy $\vec{v} = (- \frac{16}{13}; \frac{24}{13}) .$

Dạng toán 3. Dùng phép tịnh tiến để giải các bài toán dựng hình
Phương pháp:
• Để dựng một điểm $M$ ta tìm cách xem nó là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem $M$ là giao điểm của hai đường trong đó một đường cố định còn một đường là ảnh của một đường đã biết qua phép tịnh tiến.
• Sử dụng kết quả: Nếu $T_{\vec{v}} (N) = M$ và $N \in (H)$ thì $M \in (H^{'})$ , trong đó $(H^{'}) = T_{\vec{v}} ((H))$ và kết hợp với $M$ thuộc hình $(K)$ (theo giả thiết) để suy ra $M \in (H^{'}) \cap (K) .$

Ví dụ 7. Cho đường tròn tâm $O$ , bán kính $R$ và hai điểm phân biệt $C, D$ nằm ngoài $(O)$ . Hãy dựng dây cung $A B$ của đường tròn $(O)$ sao cho $A B C D$ là hình bình hành.

cac-dang-toan-phep-tinh-tien-2

Phân tích: Giả sử đã dựng được dây cung $A B$ thỏa mãn yêu cầu bài toán.
Do $A B C D$ là hình bình hành nên $\vec{A B} = \vec{D C}$ $\Rightarrow T_{\vec{C D}} (A) = B .$
Nhưng $A \in (O)$ $\Rightarrow B \in (O^{'}) = T_{\vec{D C}} ((O)) .$ Vậy $B$ vừa thuộc $(O)$ và $(O^{'})$ nên $B$ chính là giao điểm của $(O)$ và $(O^{'}) .$
Cách dựng:
+ Dựng đường tròn $(O^{'})$ là ảnh của đường tròn $(O)$ qua $T_{\vec{D C}} .$
+ Dựng giao điểm $B$ của $(O)$ và $(O^{'}) .$
+ Dựng đường thẳng qua $B$ và song song với $C D$ cắt $(O)$ tại $A .$
Dây cung $A B$ là dây cung thỏa yêu cầu bài toán.
Chứng minh: Từ cách dựng ta có $T_{\vec{D C}} (A) = B$ $\Rightarrow \vec{A B} = \vec{D C}$ $\Rightarrow A B C D$ là hình bình hành.
Nhận xét:
+ Nếu $C D > 2 R$ thì bài toán vô nghiệm .
+ Nếu $C D = 2 R$ thì có một nghiệm .
+ Nếu $C D < 2 R$ thì có hai nghiệm.

Ví dụ 8. Cho tam giác $A B C$ . Dựng đường thẳng $d$ song song với $B C$ , cắt hai cạnh $A B, A C$ lần lượt tại $M, N$ sao cho $A M = C N$ .

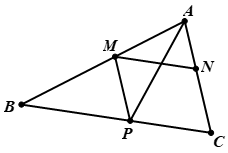
cac-dang-toan-phep-tinh-tien-3

Phân tích: Giả sử đã dựng được đường thẳng $d$ thỏa mãn bài toán. Từ $M$ dựng đường thẳng song song với $A C$ cắt $B C$ tại $P$ , khi đó $M N C P$ là hình bình hành nên $C N = P M$ . Ta lại có $A M = C N$ suy ra $M P = M A$ , từ đó ta có $A P$ là phân giác trong của góc $A .$
Cách dựng:
+ Dựng phân giác trong $A P$ của góc $A .$
+ Dựng đường thẳng đi qua $P$ song song với $A C$ cắt $A B$ tại $M .$
+ Dựng ảnh $N = T_{\vec{P M}} (C)$ .
Đường thẳng $M N$ chính là đường thẳng thỏa yêu cầu bài toán.
Chứng minh: Từ cách dựng ta có $M N C P$ là hình bình hành, suy ra $M N ∥ B C$ và $C N = P M$ , ta có $\hat{M A P} = \hat{C A P} = \hat{A P M}$ $\Rightarrow Δ M A P$ cân tại $M$ $\Rightarrow A M = M P .$ Vậy $A M = C N .$
Nhận xét: Bài toán có một nghiệm hình.

Dạng toán 4. Sử dụng phép tịnh tiến để giải các bài toán tìm tập hợp điểm
Phương pháp: Nếu $T_{\vec{v}} (M) = M^{'}$ và đểm $M$ di động trên hình $(H)$ thì điểm $M^{'}$ thuộc hình $(H^{'})$ , trong đó $(H^{'})$ là ảnh của hình $(H)$ qua $T_{\vec{v}}$ .

Ví dụ 9. Cho hai điểm phân biệt $B, C$ cố định trên đường tròn $(O)$ tâm $O$ . Điểm $A$ di động trên $(O)$ . Chứng minh khi $A$ di động trên $(O)$ thì trực tâm của tam giác $A B C$ di động trên một đường tròn.

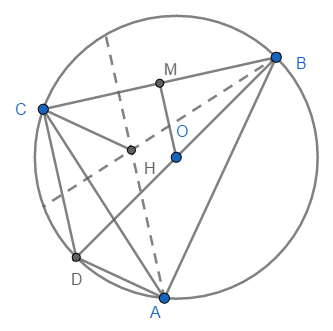
cac-dang-toan-phep-tinh-tien-4

Gọi $H$ là trực tâm của tam giác $A B C$ và $M$ là trung điểm của $B C$ . Tia $B O$ cắt đường tròn $(O)$ tại $D$ .
Vì $\hat{B C D} = 90^{0}$ , nên $D C ∥ A H$ . Tương tự $A D ∥ C H .$
Do đó $A D C H$ là hình bình hành.
Suy ra $\vec{A H} = \vec{D C} = 2 \vec{O M}$ không đổi.
$\Rightarrow T_{2 \vec{O M}} (A) = H$ .
Vì vậy khi $A$ di động trên đường tròn $(O)$ thì $H$ di động trên đường tròn $(O^{'}) = T_{2 \vec{O M}} ((O))$ .

Ví dụ 10. Cho tam giác $A B C$ có đỉnh $A$ cố định, $\hat{B A C} = α$ không đổi và $\vec{B C} = \vec{v}$ không đổi. Tìm tập hợp các điểm $B, C$ .

Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $A B C .$
Khi đó theo định lí sin ta có $\frac{B C}{\sin α} = 2 R$ không đổi (do $\vec{B C} = \vec{v}$ không đổi).
Vậy $O A = R = \frac{B C}{2 \sin α}$ , nên $O$ di động trên đường tròn tâm $A$ bán kính $A O = \frac{B C}{2 \sin α} .$
Ta có $O B = O C = R$ không đổi và $\hat{B O C} = 2 α$ không đổi suy ra $\hat{O B C} = \hat{O C B}$ $= \frac{180^{0} - 2 α}{2}$ không đổi.
Mặt khác $\vec{B C}$ có phương không đổi nên $\vec{O B}, \vec{O C}$ cũng có phương không đổi.
Đặt $\vec{O B} = \vec{v_{1}}$ , $\vec{O C} = \vec{v_{2}}$ không đổi, thì $T_{\vec{v_{1}}} (O) = B$ , $T_{\vec{v_{2}}} (O) = C .$
Vậy tập hợp điểm $B$ là đường tròn $(A_{1}; \frac{B C}{2 \sin α})$ ảnh của $(A, \frac{B C}{2 \sin α})$ qua $T_{\vec{v_{1}}}$ và tập hợp điểm $C$ là đường tròn $(A_{2}; \frac{B C}{2 \sin α})$ ảnh của $(A, \frac{B C}{2 \sin α})$ qua $T_{\vec{v_{2}}} .$