Bài viết hướng dẫn phương pháp xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp, kiến thức và các ví dụ trong bài viết được tham khảo từ các tài liệu nón – trụ – cầu đăng tải trên TOANMATH.com.
Phương pháp: Cách xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
+ Xác định trục \(d\) của đường tròn ngoại tiếp đa giác đáy (\(d\) là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
+ Xác định mặt phẳng trung trực \(\left( P \right)\) của một cạnh bên (hoặc trục \(\Delta \) của của đường tròn ngoại tiếp một đa giác của mặt bên).
+ Giao điểm \(I\) của \(\left( P \right)\) và \(d\) (hoặc của \(\Delta \) và \(d\)) là tâm mặt cầu ngoại tiếp hình chóp.
+ Bán kính của mặt cầu ngoại tiếp hình chóp là độ dài đoạn thẳng nối tâm \(I\) với một đỉnh của hình chóp.
Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.
Ta xét một số dạng hình chóp thường gặp và cách xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Dạng 1. Hình chóp có các điểm cùng nhìn một đoạn thẳng \(AB\) dưới một góc vuông.
Phương pháp:
+ Tâm: Trung điểm của đoạn thẳng \(AB\).
+ Bán kính: \(R=\frac{AB}{2}\).
Ví dụ:
• Hình chóp \(S.ABC\) có đường cao \(SA\), đáy \(ABC\) là tam giác vuông tại \(B.\)
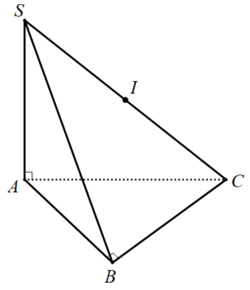
Ta có \(\widehat {SAC} = \widehat {SBC} = {90^o}\), suy ra \(A,B\) cùng nhìn \(SC\) dưới một góc vuông. Khi đó, mặt cầu ngoại tiếp hình chóp \(S.ABC\) có:
+ Tâm \(I\) là trung điểm của \(SC.\)
+ Bán kính: \(R = \frac{{SC}}{2}.\)
• Hình chóp \(S.ABCD\) có đường cao \(SA\), đáy \(ABCD\) là hình chữ nhật.

Ta có \(\widehat {SAC} = \widehat {SBC} = \widehat {SDC} = {90^o}\), suy ra \(A,B,D\) cùng nhìn \(SC\) dưới một góc vuông. Khi đó, mặt cầu ngoại tiếp hình chóp \(S.ABCD\) có:
+ Tâm \(I\) là trung điểm của \(SC.\)
+ Bán kính: \(R = \frac{{SC}}{2}.\)
Ví dụ 1: Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(SA\) vuông góc với mặt phẳng \(\left( ABC \right)\) và \(SC=2a\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\).

Ta có: \(\left\{ \begin{array}{l}
BC \bot AB\\
BC \bot SA \left( {SA \bot \left( {ABC} \right)} \right)
\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot SB.\)
\(SA \bot \left( {ABC} \right)\) \( \Rightarrow SA \bot AC.\)
Suy ra: Hai điểm \(A\), \(B\) cùng nhìn \(SC\) dưới một góc vuông.
Vậy bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) là: \(R = \frac{{SC}}{2} = a.\)
Ví dụ 2: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình vuông tại, \(SA\) vuông góc với mặt phẳng \(\left( ABCD \right)\) và \(SC=2a\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\).

Ta có: \(\left\{ \begin{array}{l}
BC \bot AB\\
BC \bot SA
\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot SB.\)
Chứng minh tương tự ta được: \(CD \bot SD.\)
\(SA \bot \left( {ABCD} \right)\) \( \Rightarrow SA \bot AC.\)
Suy ra: Ba điểm \(A\), \(B\), \(D\) cùng nhìn \(SC\) dưới một góc vuông.
Vậy bán kính mặt cầu là \(R=\frac{SC}{2}=a.\)
Dạng 2. Hình chóp đều.
Phương pháp:
• Hình chóp tam giác đều \(S.ABC\):
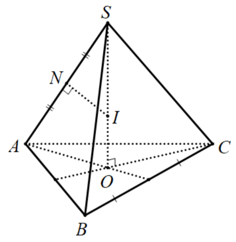
• Hình chóp tứ giác đều \(S.ABCD\):

Gọi \(O\) là tâm của đáy \(\Rightarrow SO\) là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng xác định bởi \(SO\) và một cạnh bên, chẳng hạn như \(\text{mp}\left( SAO \right)\), ta vẽ đường trung trực của cạnh \(SA\) và cắt \(SO\) tại \(I\) \(\Rightarrow I\) là tâm của mặt cầu ngoại tiếp hình chóp.
Ta có: \(\Delta SNI ∼ \Delta SOA\) \( \Rightarrow \frac{{SN}}{{SO}} = \frac{{SI}}{{SA}}\), suy ra bán kính mặt cầu ngoại tiếp hình chóp là: \(R = IS = \frac{{SN.SA}}{{SO}} = \frac{{S{A^2}}}{{2SO}}.\)
Ví dụ 3: Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều \(S.ABC\), biết các cạnh đáy có độ dài bằng \(a\), cạnh bên \(SA=a\sqrt{3}\).

Gọi \(O\) là tâm của tam giác đều \(ABC\), ta có \(SO\bot \left( ABC \right)\) nên \(SO\) là trục của đường tròn ngoại tiếp tam giác \(ABC\). Gọi \(N\) là trung điểm của \(SA\), trong \(mp\left( SAO \right)\) kẻ trung trực của \(SA\) cắt \(SO\) tại \(I\) thì \(IS\) = \(IA\) = \(IB\) = \(IC\) nên \(I\) chính là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\). Bán kính mặt cầu là \(R=SI\).
Vì hai tam giác \(SNI\) và \(SOA\) đồng dạng nên ta có \(\frac{SN}{SO}=\frac{SI}{SA}\).
Suy ra \(R=SI=\frac{SN.SA}{SO}\) \(=\frac{S{{A}^{2}}}{2SO}=\frac{3a\sqrt{6}}{8}\).
Mà \(AO=\frac{2}{3}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\), \(SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\frac{2a\sqrt{6}}{3}\).
Nên \(R=SI=\frac{3a\sqrt{6}}{8}\).
Ví dụ 4: Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng \(a\), cạnh bên bằng \(2a\).

Gọi \(O\) là tâm đáy thì \(SO\) là trục của hình vuông \(ABCD\). Gọi \(N\) là trung điểm của \(SD\), trong \(mp(SDO)\) kẻ trung trực của đoạn \(SD\) cắt \(SO\) tại \(I\) thì \(IS = IA = IB = IC = ID\) nên \(I\) là tâm của mặt cầu ngoại tiếp hình chóp \(S.ABCD\). Bán kính mặt cầu là \(R=SI\).
Ta có: \(\Delta SNI ∼ \Delta SOD\) \( \Rightarrow \frac{{SN}}{{SO}} = \frac{{SI}}{{SD}}\) \( \Rightarrow R = SI = \frac{{SD.SN}}{{SO}} = \frac{{S{D^2}}}{{2SO}}.\)
Mà \(S{O^2} = S{D^2} – O{D^2}\) \( = 4{a^2} – \frac{{{a^2}}}{2} = \frac{{7{a^2}}}{2}\) \( \Rightarrow SO = \frac{{a\sqrt 7 }}{{\sqrt 2 }}.\)
Vậy \(R = \frac{{S{D^2}}}{{2SO}} = \frac{{2a\sqrt {14} }}{7}.\)
Dạng 3. Hình chóp có cạnh bên vuông góc với mặt phẳng đáy.
Phương pháp: Cho hình chóp \(S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}\) có cạnh bên \(SA\bot \left( {{A}_{1}}{{A}_{2}}…{{A}_{n}} \right)\) và đáy \({{A}_{1}}{{A}_{2}}…{{A}_{n}}\) nội tiếp được trong đường tròn tâm \(O\). Tâm và bán kính mặt cầu ngoại tiếp hình chóp \(S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}\) được xác định như sau:
+ Từ tâm \(O\) ngoại tiếp của đường tròn đáy, ta vẽ đường thẳng \(d\) vuông góc với \(mp\left( {{A}_{1}}{{A}_{2}}…{{A}_{n}} \right)\) tại \(O\).
+ Trong \(mp\left( d,S{{A}_{1}} \right)\), ta dựng đường trung trực \(\Delta \) của cạnh \(SA\), cắt \(S{{A}_{1}}\) tại \(N\), cắt \(d\) tại \(I\).
+ Khi đó: \(I\) là tâm mặt cầu ngoại tiếp hình chóp, bán kính \(R=I{{A}_{1}}=I{{A}_{2}}=…=I{{A}_{n}}=IS\).
+ Tìm bán kính: Ta có: \(MIO{A_1}\) là hình chữ nhật, xét \(\Delta M{A_1}I\) vuông tại \(M\) có: \(R = {A_1}I = \sqrt {M{I^2} + M{A_1}^2} \) \( = \sqrt {{A_1}{O^2} + {{\left( {\frac{{S{A_1}}}{2}} \right)}^2}} .\)

Ví dụ 5: Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với đáy, \(ABC\) là tam giác vuông tại \(A\), biết \(AB=6a\), \(AC=8a\), \(SA=10a\). Tìm bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\).

Gọi \(O\) là trung điểm của cạnh \(BC\). Suy ra \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) vuông tại \(A\).
Dựng trục \(d\) của đường tròn ngoại tiếp tam giác \(ABC\); trong mặt phẳng \(\left( SA,d \right)\) vẽ trung trực cạnh \(SA\) và cắt \(d\) tại \(I\).
Suy ra \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) và bán kính \(R=IA=IB=IC=IS\).
Ta có tứ giác \(NIOA\) là hình chữ nhật.
Xét tam giác \(NAI\) vuông tại \(N\) có: \(R = IA = \sqrt {N{I^2} + N{A^2}} \) \( = \sqrt {A{O^2} + {{\left( {\frac{{SA}}{2}} \right)}^2}} \) \( = \sqrt {{{\left( {\frac{{BC}}{2}} \right)}^2} + {{\left( {\frac{{SA}}{2}} \right)}^2}} \) \( = \sqrt {\frac{{A{B^2} + A{C^2}}}{4} + {{\left( {\frac{{SA}}{2}} \right)}^2}} \) \( = 5a\sqrt 2 .\)
Ví dụ 6: Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với đáy, \(ABC\) là tam giác đều cạnh bằng \(a\), \(SA=2a\). Tìm bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\).

Gọi \(O\) là trọng tâm của tam giác \(ABC\). Suy ra \(O\) là tâm đường tròn ngoại tiếp tam giác đều \(ABC\).
Dựng trục \(d\) của đường tròn ngoại tiếp tam giác \(ABC\); trong mặt phẳng \(\left( SA,d \right)\) vẽ trung trực cạnh \(SA\) và cắt \(d\) tại \(I\).
Suy ra \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) và bán kính \(R=IA=IB=IC=IS\).
Ta có tứ giác \(NIOA\) là hình chữ nhật.
Xét tam giác \(NAI\) vuông tại \(N\) có: \(R = IA = \sqrt {N{I^2} + N{A^2}} \) \( = \sqrt {A{O^2} + {{\left( {\frac{{SA}}{2}} \right)}^2}} \) \( = \sqrt {{{\left( {\frac{2}{3} \cdot \frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{2a}}{2}} \right)}^2}} \) \( = \frac{{2a\sqrt 3 }}{3}.\)
Ví dụ 7: Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với đáy, \(ABC\) là tam giác cân tại \(A\) và \(AB=a\), \(\widehat{BAC}=120^o \), \(SA=2a\). Tính bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\).

Gọi \(O\) là tâm đường tròn ngoại tiếp của tam giác \(ABC\).
Dựng trục \(d\) của đường tròn ngoại tiếp tam giác \(ABC\); trong mặt phẳng \(\left( SA,d \right)\) vẽ trung trực cạnh \(SA\) và cắt \(d\) tại \(I\).
Suy ra \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) và bán kính \(R=IA=IB=IC=IS\).
Mặt khác, ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A\) \( = \frac{{{a^2}\sqrt 3 }}{4}\) và \(BC = \sqrt {A{B^2} + A{C^2} – 2AB.AC.\cos {\rm{A}}} \) \( = a\sqrt 3 .\)
\(OA\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\) nên \(OA = \frac{{AB.BC.CA}}{{4{S_{ABC}}}} = a.\)
Tứ giác \(NIOA\) là hình chữ nhật nên \(NI=OA=a\).
Xét tam giác \(NAI\) vuông tại \(N\) có: \(R = IA = \sqrt {N{I^2} + N{A^2}} \) \( = \sqrt {A{O^2} + {{\left( {\frac{{SA}}{2}} \right)}^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 .\)
Dạng 4. Hình chóp có mặt bên vuông góc với mặt phẳng đáy.
Đối với dạng toán này thì mặt bên vuông góc thường là tam giác vuông, tam giác cân hoặc tam giác đều.
Phương pháp:
+ Xác định trục \(d\) của đường tròn đáy.
+ Xác định trục \(\Delta \) của đường tròn ngoại tiếp mặt bên vuông góc với đáy.
+ Giao điểm \(I\) của \(d\) và \(\Delta \) là tâm mặt cầu ngoại tiếp hình chóp.

Xét hình chóp \(S.{{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\) có mặt bên vuông góc với mặt đáy, không mất tính quát ta giả sử mặt bên \(\left( S{{A}_{1}}{{A}_{2}} \right)\) vuông góc với mặt đáy và \(\Delta S{{A}_{1}}{{A}_{2}}\) là tam giác vuông hoặc tam giác cân hoặc tam giác đều.
Gọi \({{O}_{1}}\) và \({{O}_{2}}\) lần lượt là tâm đường tròn ngoại tiếp đa giác \({{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\) và tam giác \(S{{A}_{1}}{{A}_{2}}\).
Dựng \(d\) và \(\Delta \) lần lượt là trục đường tròn ngoại tiếp đa giác \({{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\) và tam giác \(S{{A}_{1}}{{A}_{2}}\).
Gọi \(I\) là giao điểm của \(d\) và \(\Delta \) thì \(I\) cách đều các đỉnh \({{A}_{1}}\), \({{A}_{2}}\), …, \({{A}_{n}}\) và \(S\) nên \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.{{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\).
Ta có tứ giác \({{O}_{2}}I{{O}_{1}}H\) là hình chữ nhật; \(SI=R\) là bán kính mặt cầu ngoại tiếp \(S.{{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\); \(S{{O}_{2}}={{R}_{b}}\) là bán kính đường tròn ngoại tiếp tam giác \(S{{A}_{1}}{{A}_{2}}\); \({{A}_{1}}{{O}_{1}}={{R}_{đ}}\) là bán kính đường tròn ngoại tiếp đa giác \({{A}_{1}}{{A}_{2}}\cdots {{A}_{n}}\).
Tam giác \(S{{O}_{2}}I\) vuông tại \({{O}_{2}}\) nên: \(SI = \sqrt {SO_2^2 + {O_2}{I^2}} \) \( = \sqrt {SO_2^2 + {O_1}{H^2}} .\)
Tam giác \({{A}_{1}}{{O}_{1}}H\) vuông tại \(H\) nên: \({O_1}{H^2} = {O_1}A_1^2 – {A_1}{H^2}.\)
Do đó: \(SI = \sqrt {SO_2^2 + {O_1}A_1^2 – {A_1}{H^2}} .\)
Mặt khác, nếu tam giác \(S{{A}_{1}}{{A}_{2}}\) vuông tại \(S\) thì \({{O}_{2}}\equiv H\) và trùng với trung điểm \({{A}_{1}}{{A}_{2}}\) hoặc \(S{{A}_{1}}{{A}_{2}}\) là tam giác cân tại \(S\) hoặc đều thì ta cũng có \(H\) trùng với trung điểm \({{A}_{1}}{{A}_{2}}\) nên \({{A}_{1}}H=\frac{{{A}_{1}}{{A}_{2}}}{2}\).
Suy ra \(SI = \sqrt {SO_2^2 + {O_1}A_1^2 – {{\left( {\frac{{{A_1}{A_2}}}{2}} \right)}^2}} .\)
Hay \(R = \sqrt {{R_b}^2 + {R_đ}^2 – \frac{{{\partial ^2}}}{4}} \), với \(\partial \) là độ dài cạnh cạnh chung của mặt bên vuông góc với đáy.
Ví dụ 8: Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\). Mặt bên \(\left( SAB \right)\bot \left( ABC \right)\) và \(\Delta SAB\) đều cạnh bằng \(1\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\).

Gọi \(H\), \(M\) lần lượt là trung điểm của \(AB\), \(AC\).
Ta có \(M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) (do \(MA=MB=MC\)).
Dựng \(d\) là trục đường tròn ngoại tiếp \(\Delta ABC\) (\(d\) qua \(M\) và song song \(SH\)).
Gọi \(G\) là tâm đường tròn ngoại tiếp \(\Delta SAB\) và \(\Delta \) là trục đường tròn ngoại tiếp \(\Delta SAB\), \(\Delta \) cắt \(d\) tại \(I\). Suy ra \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\).
Suy ra bán kính \(R=SI\). Xét \(\Delta SGI\), suy ra \(SI=\sqrt{G{{I}^{2}}+S{{G}^{2}}}\).
Mà \(SG=\frac{1}{\sqrt{3}}\); \(GI=HM=\frac{1}{2}AC=\frac{1}{2}\).
Nên \(R=SI=\sqrt{\frac{1}{3}+\frac{1}{4}}=\frac{\sqrt{21}}{6}\).
Ví dụ 9: Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(1\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích \(V\) của khối cầu ngoại tiếp hình chóp đã cho.
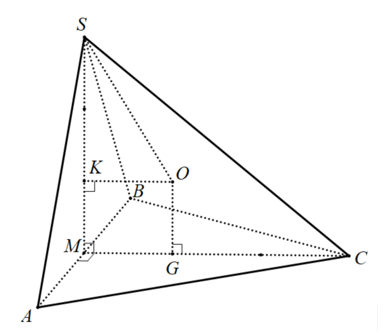
Gọi \(M\) là trung điểm của \(AB\) thì \(SM\bot AB\) (vì tam giác \(SAB\) đều). Mặt khác do \(\left( SAB \right)\bot (ABC)\) nên \(SM\bot (ABC)\).
Tương tự: \(CM\bot (SAB)\).
Gọi \(G\) và \(K\) lần lượt là tâm của các tam giác \(ABC\) và \(SAB\).
Trong mặt phẳng \((SMC)\), kẻ đường thẳng \(Gx\text{//}SM\) và kẻ đường thẳng \(Ky\bot SM\).
Gọi \(O=Gx\cap Ky\), thì ta có: \(\left\{ \begin{array}{l}
OG \bot (SAB)\\
OK \bot (ABC)
\end{array} \right.\)
Suy ra \(OG,OK\) lần lượt là trục của tam giác \(ABC\) và \(SAB\).
Do đó ta có: \(OA=OB=OC=OD=OS\) hay \(O\) chính là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\).
Tứ giác \(OKMN\) là hình chữ nhật có \(MK=MG=\frac{\sqrt{3}}{6}\) nên \(OKMN\) là hình vuông.
Do đó \(OK=\frac{\sqrt{3}}{6}\).
Mặt khác \(SK=\frac{\sqrt{3}}{3}\). Xét tam giác \(SKO\) vuông tại \(K\) có \(OS = \sqrt {O{K^2} + S{K^2}} \) \( = \sqrt {\frac{3}{{36}} + \frac{3}{9}} = \frac{{\sqrt {15} }}{6}.\)
Suy ra bán kính mặt cầu cần tìm là \(R=OS=\frac{\sqrt{15}}{6}\). Vậy thể tích khối cầu cần tìm là:
\(V = \frac{4}{3}\pi {R^3}\) \( = \frac{4}{3}\pi .{\left( {\frac{{\sqrt {15} }}{6}} \right)^3}\) \( = \frac{{5\sqrt {15} \pi }}{{54}}.\)
Nguồn: toanmath.com
