Bài viết trình bày phương pháp xác định và tính góc giữa hai đường thẳng chéo nhau trong không gian bằng cách sử dụng hình học không gian cổ điển, đây là một nội dung thường gặp trong chương trình Hình học 11 chương 3: Quan hệ vuông góc, kiến thức và các ví dụ trong bài viết được tham khảo từ các tài liệu hình học không gian được chia sẻ trên TOANMATH.com.
Bài toán: Cho hai đường thẳng \(a\) và \(b\) chéo nhau, xác định góc giữa \(2\) đường thẳng \(a\) và \(b.\)
Để xác định góc giữa hai đường thẳng \(a\) và \(b\) chéo nhau, ta sử dụng các cách sau:
Cách 1: Chọn hai đường thẳng cắt nhau \(a’\) và \(b’\) lần lượt song song với \(a\) và \(b\). Khi đó \((\widehat {a,b}) = (\widehat {a’,b’})\).
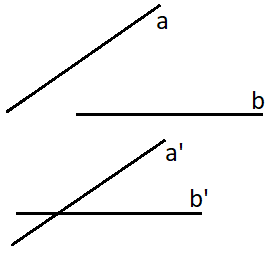
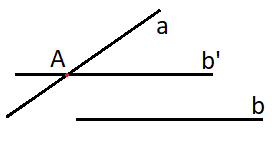
Cách 2: Chọn một điểm \(A\) bất kỳ thuộc \(a\), rồi từ đó kẻ một đường thẳng \(b’\) qua \(A\) và song song với \(b\). Khi đó \((\widehat {a,b}) = (\widehat {a,b’})\).
Ví dụ 1: Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\), \(SA = a\sqrt 3 ,SA \bot BC\). Tính góc giữa hai đường thẳng \(SD\) và \(BC\)?
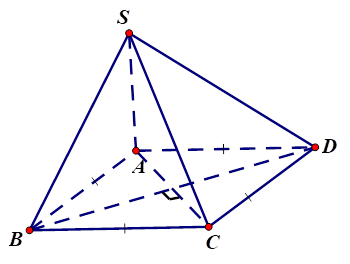
Ta có: \(BC//AD.\)
Do đó \((SD,BC) = (SD,AD) = \widehat {SDA}.\)
Vì \(\left. \begin{array}{l}
BC||AD\\
SA \bot BC
\end{array} \right\}\) \( \Rightarrow SA \bot AD \Rightarrow \widehat {SAD} = {90^0}.\)
Xét tam giác \(ΔSAD\) vuông tại \(A\) ta có:
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \sqrt 3 \) \( \Rightarrow \widehat {SDA} = {60^0}.\)
Vậy góc giữa hai đường thẳng \(SD\) và \(BC\) bằng \(60\) độ.
Ví dụ 2: Cho tứ diện \(ABCD\) có \(AB = CD = 2a\). Gọi \(M, N\) lần lượt là trung điểm của \(BC\) và \(AD\), \(MN = a\sqrt 3 \). Tính góc giữa hai đường thẳng \(AB\) và \(CD\)?

Gọi \(I\) là trung điểm của \(BD.\)
Ta có: \(\left. \begin{array}{l}
IN//AB\\
IM//CD
\end{array} \right\}\) \( \Rightarrow (AB,CD) = (IM,IN).\)
Xét tam giác \(IMN\) có:
\(IM = IN = a,MN = a\sqrt 3 .\)
Do đó \(\cos \widehat {MIN} = \frac{{2{a^2} – 3{a^2}}}{{2{a^2}}} = – \frac{1}{2}\) \( \Rightarrow \widehat {MIN} = {120^0}.\)
Vậy \((\widehat {AB,CD}) = {180^0} – {120^0} = {60^0}\).
Ví dụ 3: Cho hình lăng trụ \(ABC.A’B’C’\) có độ dài cạnh bên bằng \(2a\), đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a,AC = a\sqrt 3\). Hình chiếu vuông góc của \(A’\) lên \(mp(ABC)\) là trung điểm của \(BC\). Tính \(cosin\) của góc giữa hai đường thẳng \(AA’\) và \(B’C’\)?
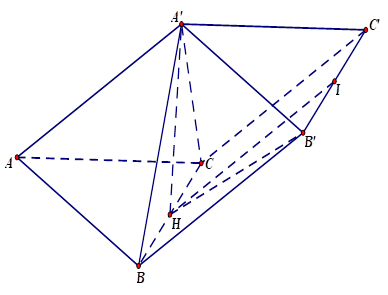
Gọi \(H\) là trung điểm của \(BC.\)
Ta có: \(\left. \begin{array}{l}
AA’//BB’\\
B’C’//BH
\end{array} \right\}\) \( \Rightarrow (AA’,B’C’) = (BB’,BH).\)
Hay \(\cos (AA’,B’C’) = \cos (BB’,BH)\) \( = \left| {\cos \widehat {HBB’}} \right|.\)
Xét tam giác \(A’B’H\) có:
\(\widehat {A’} = {90^0},A’B’ = a.\)
\(A’H = \sqrt {AA{‘^2} – A{H^2}} \) \( = \sqrt {AA{‘^2} – {{\left( {\frac{{BC}}{2}} \right)}^2}} = a\sqrt 3 .\)
Suy ra \(HB’ = \sqrt {A'{H^2} + A’B{‘^2}} = 2a.\)
Do đó \(\cos \widehat {HBB’} = \frac{{B{H^2} + BB{‘^2} – HB{‘^2}}}{{2.BH.BB’}} = \frac{1}{4}.\)
Vậy \(\cos (AA’,B’C’) = \left| {\cos \widehat {HBB’}} \right| = \frac{1}{4}\).
Nguồn: toanmath.com
