Bài viết trình bày lý thuyết, công thức và các ví dụ có lời giải chi tiết về phương pháp tính thể tích khối lăng trụ, đây là dạng toán thường gặp trong chương trình Hình học 12 chương 1.
Phương pháp tính thể tích khối lăng trụ
Công thức:
• Thể tích khối lăng trụ: \(V = B.h\).
• Thể tích khối hộp chữ nhật có các cạnh \(a, b, c\): \(V = abc\).
• Thể tích khối lập phương cạnh \(a\): \(V = a^3\).
Để tính thể tích của khối lăng trụ ta cần đi tính chiều cao của lăng trụ và diện tích đáy.
Các tính chất của lăng trụ:
a. Hình lăng trụ
• Các cạnh bên của hình lăng trụ song song và bằng nhau.
• Các mặt bên của hình lăng trụ là các hình bình hành.
• Hai đáy của hình lăng trụ là hai đa giác bằng nhau và nằm trong hai mặt phẳng song song với nhau.
• Lăng trụ có các cạnh bên vuông góc hai đáy được gọi là lăng trụ đứng.
* Các cạnh bên của lăng trụ đứng chính là đường cao của nó.
* Các mặt bên của lăng trụ đứng là các hình chữ nhật.
• Lăng trụ đứng có đáy là đa giác đều được gọi là lăng trụ đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau.
b. Hình hộp: Là hình lăng trụ có đáy là hình bình hành:
• Hình hộp đứng có các cạnh bên vuông góc với đáy.
• Hình hộp đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
• Hình hộp chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương.
• Đường chéo của hình hộp chữ nhật có ba kích thước \(a, b, c\) là: \(d = \sqrt {a^2 + b^2 + c^2}.\)
• Đường chéo của hình lập phương cạnh \(a\) là \(d = a \sqrt 3.\)
Các dạng toán thể tích khối lăng trụ
Dạng 1: Khối lăng trụ đứng có chiều cao hay cạnh đáy
Ví dụ 1: Đáy của lăng trụ đứng tam giác \(ABC.A’B’C’\) là tam giác \(ABC\) vuông cân tại \(A\) có cạnh \(BC = a\sqrt 2 \) và biết \(A’B = 3a\). Tính thể tích khối lăng trụ.

Ta có:
\(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC = a.\)
\(ABC.A’B’C’\) là lăng trụ đứng \( \Rightarrow AA’ \bot AB\), do đó \(\Delta AA’B\) vuông tại \(A\) nên: \(AA{‘^2} = A'{B^2} – A{B^2} = 8{a^2}\) \( \Rightarrow AA’ = 2a\sqrt 2 .\)
Vậy \(V = {S_{\Delta ABC}}.AA’ = {a^3}\sqrt 2 .\)
Ví dụ 2: Cho lăng trụ tứ giác đều \(ABCD.A’B’C’D’\) có cạnh bên bằng \(4a\) và đường chéo \(5a\). Tính thể tích khối lăng trụ này.

\(ABCD.A’B’C’D’\) là lăng trụ đứng nên \(ΔBDD’\) vuông tại \(D\), do đó: \(BD^2 = BD’^2 – DD’^2 = 9a^2\) \( \Rightarrow BD = 3a.\)
\(ABCD\) là hình vuông \( \Rightarrow AB = \frac{{3a}}{{\sqrt 2 }}.\)
Suy ra \({S_{ABCD}} = \frac{{9{a^2}}}{4}.\)
Vậy \(V = S_{ABCD}.AA’ = 9a^3.\)
Ví dụ 3: Đáy của lăng trụ đứng tam giác \(ABC.A’B’C’\) là tam giác đều cạnh \(a = 4\) và biết diện tích tam giác \(A’BC\) bằng \(8\). Tính thể tích khối lăng trụ.
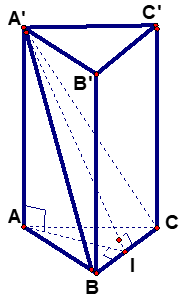
Gọi \(I\) là trung điểm \(BC\). Ta có:
\(ΔABC\) đều nên \(AI = \frac{{AB\sqrt 3 }}{2} = 2\sqrt {3} \) và \(AI \bot BC\) \( \Rightarrow A’I \bot BC\) (theo định lý ba đường vuông góc).
\({S_{A’BC}} = \frac{1}{2}BC.A’I\) \( \Rightarrow A’I = \frac{{2{S_{A’BC}}}}{{BC}} = 4.\)
\(AA’ \bot (ABC) \Rightarrow AA’ \bot AI.\)
\(\Delta A’AI\) vuông tại \(A\) nên \( \Rightarrow AA’ = \sqrt {A'{I^2} – A{I^2}} = 2.\)
Vậy: \({V_{ABC.A’B’C’}} = {S_{ABC}}.AA’ = 8\sqrt 3 .\)
Ví dụ 4: Cho hình hộp đứng có đáy là hình thoi cạnh \(a\) và có góc nhọn bằng \(60°.\) Đường chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ. Tính thể tích hình hộp.

Xác định các điểm như hình vẽ.
Ta có tam giác \(ΔABD\) đều nên \(BD = a\), \({S_{ABCD}} = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}.\)
Theo đề bài \(BD’ = AC = 2\frac{{a\sqrt 3 }}{2} = a\sqrt 3 .\)
\(\Delta DD’B\) vuông tại \(D\) \( \Rightarrow DD’ = \sqrt {BD{‘^2} – B{D^2}} = a\sqrt 2 .\)
Vậy \(V = {S_{ABCD}}.DD’ = \frac{{{a^3}\sqrt 6 }}{2}.\)
Dạng 2: Lăng trụ đứng có góc giữa đường thẳng và mặt phẳng
Ví dụ 5: Cho lăng trụ đứng tam giác \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) với \(BA = BC = a\), biết \(A’B\) hợp với đáy \(ABC\) một góc \(60°.\) Tính thể tích lăng trụ.

Ta có \(A’A \bot (ABC)\) nên \(AB\) là hình chiếu của \(A’B\) trên đáy \((ABC)\), suy ra góc \(\left( {\widehat {A’B,(ABC)}} \right) = \widehat {ABA’} = {60^o}.\)
\(A’A \bot AB\) nên \(\Delta ABA’\) vuông tại \(A\) \( \Rightarrow AA’ = AB.\tan {60^0} = a\sqrt 3 .\)
\({S_{ABC}} = \frac{1}{2}BA.BC = \frac{{{a^2}}}{2}.\)
Vậy \(V = {S_{ABC}}.AA’ = \frac{{{a^3}\sqrt 3 }}{2}.\)
Ví dụ 6: Cho lăng trụ đứng tam giác \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A\) với \(AC = a\), \(\widehat {ACB} = {60^o}\), biết \(BC’\) hợp với \((AA’C’C)\) một góc \(30°\). Tính \(AC’\) và thể tích lăng trụ.
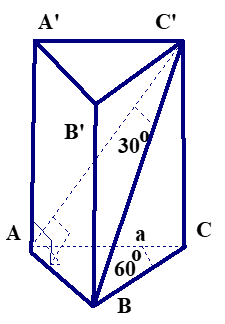
\(\Delta ABC\) vuông tại \(A\) \( \Rightarrow AB = AC.\tan {60^o} = a\sqrt 3 .\)
Ta có: \(AB \bot AC; AB \bot AA’\) \( \Rightarrow AB \bot (AA’C’C)\) nên \(AC’\) là hình chiếu của \(BC’\) trên \((AA’C’C).\)
Do đó \(\widehat {\left( {BC’;\left( {AA’C’C} \right)} \right)} = \widehat {BC’A} = 30°.\)
\(\Delta AC’B\) vuông tại \(A\) \( \Rightarrow AC’ = \frac{{AB}}{{{\mathop{\rm t}\nolimits} {\rm{an}}{{30}^o}}} = 3a.\)
\(\Delta AA’C’\) vuông tại \(A’\) \( \Rightarrow AA’ = \sqrt {AC’^2 – A’C’^2} = 2a\sqrt 2 .\)
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{{{a^2}\sqrt 3 }}{2}.\)
Vậy \(V = {S_{ABC}}.AA’ = {a^3}\sqrt 6 .\)
Ví dụ 7: Cho lăng trụ đứng \(ABCD.A’B’C’D’\) có đáy \(ABCD\) là hình vuông cạnh \(a\) và đường chéo \(BD’\) của lăng trụ hợp với đáy \(ABCD\) một góc \(30°\). Tính thể tích và tổng diên tích của các mặt bên của lăng trụ.

Ta có \(ABCD.A’B’C’D’\) là lăng trụ đứng nên \(BD\) là hình chiếu của \(BD’\) trên \((ABCD).\)
Suy ra \(\widehat {\left( {BD’;\left( {ABCD} \right)} \right)} = \widehat {DBD’} = {30^o}.\)
\(\Delta BDD’\) vuông tại \(D\) \( \Rightarrow DD’ = BD.\tan {30^0} = \frac{{a\sqrt 6 }}{3}.\)
Vậy \(V = {S_{ABCD}}.DD’ = \frac{{{a^3}\sqrt 6 }}{3}.\)
\(S = 4{S_{ADD’A’}} = \frac{{4{a^2}\sqrt 6 }}{3}.\)
Dạng 3: Lăng trụ đứng có góc giữa 2 mặt phẳng
Ví dụ 8: Cho lăng trụ đứng tam giác \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) với \(BA = BC = a\), biết \((A’BC)\) hợp với đáy \((ABC)\) một góc \(60°\).Tính thể tích lăng trụ.
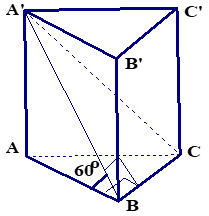
Ta có: \(AA’ \bot (ABC) \Rightarrow BC \bot AA’.\)
Mà \(BC \bot AB\) nên \(BC \bot (ABA’).\)
Suy ra \(BC \bot A’B.\)
Do đó \(\widehat {\left( {(A’BC),(ABC)} \right)} = \widehat {ABA’} = {60^o}.\)
\(\Delta ABA’\) vuông tại \(A\) nên \(AA’ = AB.\tan {60^0} = a\sqrt 3 .\)
\({S_{ABC}} = \frac{1}{2}BA.BC = \frac{{{a^2}}}{2}.\)
Vậy \(V = {S_{ABC}}.AA’ = \frac{{{a^3}\sqrt 3 }}{2}.\)
Ví dụ 9: Đáy của lăng trụ đứng tam giác \(ABC.A’B’C’\) là tam giác đều. Mặt phẳng \((A’BC)\) tạo với đáy một góc \(30°\) và diện tích tam giác \(A’BC\) bằng \(8\). Tính thể tích khối lăng trụ.

Gọi \(I\) là trung điểm của \(BC.\)
\(\Delta ABC\) đều \( \Rightarrow AI \bot BC\), mà \(AA’ \bot (ABC)\) nên \(A’I \bot BC\) (định lý \(3\) đường vuông góc).
Do đó: \(\widehat {\left( {\left( {A’BC} \right);\left( {ABC} \right)} \right)} = \widehat {A’IA} = {30^o}.\)
Giả sử \(BI = x\), suy ra \(AI = x \sqrt 3\).
Ta có: \(ΔA’AI\) vuông tại \(A\) nên \(A’I = AI.\cos{30°} = 2x\) và \(A’A = AI.\tan {30°} = x.\)
\(S_{A’BC} = BI.A’I = x.2x = 8\), suy ra \(x = 2.\)
Vậy \(V_{ABC.A’B’C’} = BI.AI.A’A = 8√3 .\)
Ví dụ 10: Cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có \(AA’ = 2a\); mặt phẳng \((A’BC)\) hợp với đáy \((ABCD)\) một góc \(60°\)và \(A’C\) hợp với đáy \((ABCD)\) một góc \(30°\).Tính thể tích khối hộp chữ nhật.
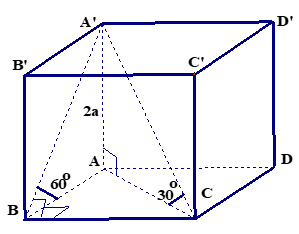
Ta có \(AA’ \bot (ABCD)\), suy ra \(AC\) là hình chiếu của \(A’C\) trên \((ABCD).\)
Nên \(\widehat {\left( {A’C,\left( {ABCD} \right)} \right)} = \widehat {A’CA} = {30^o}.\)
\(BC \bot (ABB’A’)\) nên \(\widehat {\left( {A’BC} \right),\left( {ABCD} \right)} = \widehat {A’BA} = {60^o}.\)
\(\Delta A’AC\) vuông tại \(A\) nên \(AC = AA’.cot{30^o} = 2a\sqrt 3 .\)
\(\Delta A’AB\) vuông tại \(A\) nên \(AB = AA’.cot{60^o} = \frac{{2a\sqrt 3 }}{3}.\)
\(\Delta ABC\) vuông tại \(B\) nên \( \Rightarrow BC = \sqrt {A{C^2} – A{B^2}} = \frac{{4a\sqrt 6 }}{3}.\)
Vậy: \(V = AB.BC.AA’ = \frac{{16{a^3}\sqrt 2 }}{3}.\)
Dạng 4: Khối lăng trụ xiên
Ví dụ 11: Cho lăng trụ xiên tam giác \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác đều cạnh \(a\), biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy \(ABC\) một góc \(60°\). Tính thể tích lăng trụ.
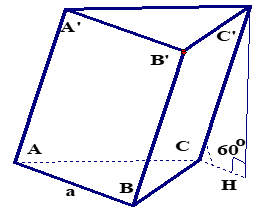
Gọi \(H\) là hình chiếu vuông góc của \(C’\) lên \((ABC)\).
Khi đó \(\widehat {\left( {CC’,(ABC)} \right)} = \widehat {C’CH} = {60^o}.\)
\(\Delta CHC’\) vuông tại \(H\) \( \Rightarrow C’H = CC’.\sin {60^0} = \frac{{3a}}{2}.\)
\({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}.\)
Vậy \(V = {S_{ABC}}.C’H = \frac{{3{a^3}\sqrt 3 }}{8}.\)
Ví dụ 12: Cho lăng trụ xiên tam giác \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu của \(A’\) xuống \((ABC)\) là tâm \(O\) đường tròn ngoại tiếp tam giác \(ABC\) biết \(AA’\) hợp với đáy \((ABC)\) một góc \(60°.\)
1. Chứng minh rằng \(BB’C’C\) là hình chữ nhật.
2. Tính thể tích lăng trụ.
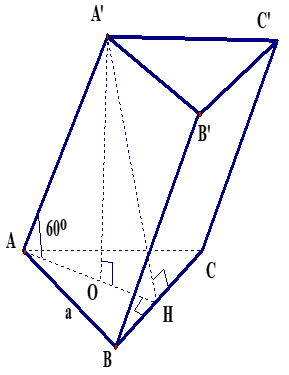
1. Ta có \(BB’C’C\) là hình bình hành vì là mặt bên của lăng trụ.
Gọi \(H\) là trung điểm của \(BC\), vì tam giác \(ΔABC\) đều nên \(O ∈ AH.\)
Ta có: \(BC \bot AH\) và \(BC \bot A’O\) nên \(BC \bot (AAH)’\), do đó \(BC \bot A’A.\)
Mà \(AA’ // BB’\), do đó \(BC \bot BB’\), suy ra \(BB’C’C\) là hình chữ nhật.
2. \(\Delta ABC\) đều nên \(AO = \frac{2}{3}AH = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}.\)
\(\Delta AOA’\) vuông tại \(O\) \( \Rightarrow A’O = AO\tan {60^o} = a.\)
Vậy \(V = {S_{ABC}}.A’O = \frac{{{a^3}\sqrt 3 }}{4}.\)
Ví dụ 13: Cho hình hộp \(ABCD.A’B’C’D’\) có đáy là hình chữ nhật với \(AB = \sqrt 3\), \(AD = \sqrt 7\). Hai mặt bên \((ABB’A’)\) và \((ADD’A’)\) lần lượt tạo với đáy những góc \(45°\) và \(60°\). Tính thể tích khối hộp nếu biết cạnh bên bằng \(1.\)

Kẻ \(A’H \bot (ABCD)\), \(HM \bot AB\), \(HN \bot AD\) (các điểm nằm trên các đường thẳng và mặt phẳng như hình vẽ).
Khi đó \(A’M \bot AB\) và \(A’N \bot AD.\)
Suy ra: \( \widehat {A’MH} = {45^o}, \widehat {A’NH} = {60^o}.\)
Đặt \(A’H = x\).
\(ΔA’HN\) vuông tại \(H\) nên \(A’N = x : sin 60° = \frac{{2x}}{{\sqrt 3 }}.\)
\(ΔA’AN\) vuông tại \(N\) nên \(AN = \sqrt {AA{‘^2} – A'{N^2}} = \sqrt {\frac{{3 – 4{x^2}}}{3}} .\)
\(ΔA’MH\) vuông tại \(H\) nên \(HM = x.cot{45^0} = x.\)
Vì tứ giác \(AMHN\) là hình chữ nhật nên \(AN = MH\), suy ra: \(\sqrt {\frac{{3 – 4{x^2}}}{3}} = x\) \( \Leftrightarrow x = \sqrt {\frac{3}{7}} .\)
Vậy \({V_{ABCD.A’B’C’D’}} = AB.AD.A’H = 3.\)
Nguồn: toanmath.com
