Bài viết hướng dẫn các bước khảo sát và vẽ đồ thị hàm số bậc ba (bậc 3) $y = a{x^3} + b{x^2} + cx + d$ với $a ≠ 0$, cùng với đó là lời giải chi tiết một số dạng toán liên quan. Kiến thức và các ví dụ minh họa trong bài viết được tham khảo từ các tài liệu về chuyên đề hàm số xuất bản trên TOANMATH.com.
Phương pháp: Các bước khảo sát và vẽ đồ thị hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d$ với $a ≠ 0.$
+ Bước 1. Tập xác định: $D = R.$
+ Bước 2. Đạo hàm: $y’ = 3a{x^2} + 2bx + c$, $\Delta’ = {b^2} – 3ac.$
$\Delta’ > 0$: Hàm số có $2$ cực trị.
$\Delta’ \le 0$: Hàm số luôn tăng hoặc luôn giảm trên $R$.
+ Bước 3. Đạo hàm cấp $2$: $y” = 6ax + 2b$, $y” = 0 \Leftrightarrow x = – \frac{b}{{3a}}.$
$x = – \frac{b}{{3a}}$ là hoành độ điểm uốn, đồ thị nhận điểm uốn làm tâm đối xứng.
+ Bước 4. Giới hạn:
Nếu $a > 0$ thì: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$
Nếu $a < 0$ thì: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$
+ Bước 5. Bảng biến thiên và đồ thị:
Trường hợp $a > 0$:
+ $\Delta’ = {b^2} – 3ac > 0$: Hàm số có $2$ cực trị.
+ $\Delta’ = {b^2} – 3ac \le 0$ $ \Rightarrow y’ \ge 0,\forall x \in R$: Hàm số luôn tăng trên $R$.
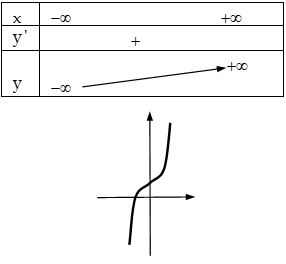
Trường hợp $a < 0$:
+ $\Delta’ = {b^2} – 3ac > 0$: Hàm số có $2$ cực trị.
+ $\Delta’ = {b^2} – 3ac \le 0$ $ \Rightarrow y’ \le 0,\forall x \in R$: Hàm số luôn giảm trên $R$.
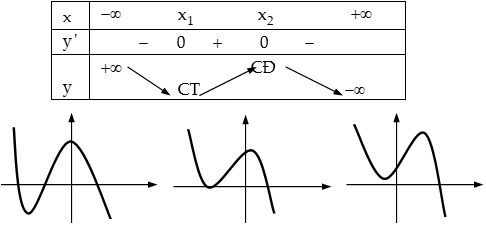
Một số tính chất của hàm số bậc ba
1. Hàm số có cực đại và cực tiểu khi và chỉ khi: $\Delta’ = {b^2} – 3ac > 0$.
2. Hàm số luôn đồng biến trên $R$ $ \Leftrightarrow \left\{ \begin{array}{l}
a > 0\\
\Delta’ = {b^2} – 3ac \le 0
\end{array} \right.$
3. Hàm số luôn nghịch biến trên $R$ $ \Leftrightarrow \left\{ \begin{array}{l}
a < 0\\
\Delta’ = {b^2} – 3ac \le 0
\end{array} \right.$
4. Để tìm giá cực trị (đường thẳng đi qua $2$ điểm cực trị) ta lấy $f(x)$ chia cho $f'(x)$: $f(x) = f'(x).g(x) + rx + q$. Nếu ${x_1}, {x_2}$ là hai nghiệm của $f'(x)$ thì: $f({x_1}) = r{x_1} + q$, $f({x_2}) = r{x_2} + q.$ Khi đó đường thẳng đi qua các điểm cực trị là $y = rx + q$.
5. Đồ thị luôn có điểm uốn $I$ và là tâm đối xứng của đồ thị.
6. Đồ thị cắt $Ox$ tại $3$ điểm phân biệt $ \Leftrightarrow $ hàm số có hai cực trị trái dấu nhau.
7. Đồ thị cắt $Ox$ tại hai điểm phân biệt $ \Leftrightarrow $ đồ thị hàm số có hai cực trị và một cực trị nằm trên $Ox$.
8. Đồ thị cắt $Ox$ tại một điểm $ \Leftrightarrow $ hoặc hàm số không có cực trị hoặc hàm số có hai cực trị cùng dấu.
9. Tiếp tuyến: Gọi $I$ là điểm uốn. Cho $M \in (C).$
+ Nếu $M \equiv I$ thì có đúng một tiếp tuyến đi qua $M$ và tiếp tuyến này có hệ số góc nhỏ nhất (nếu $a > 0$), lớn nhất (nếu $a < 0$).
+ Nếu $M$ khác $I$ thì có đúng $2$ tiếp tuyến đi qua $M$.
[ads]
Ví dụ minh họa
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số:
a. $y = – {x^3} + 3{x^2} – 4.$
b. $y = – {x^3} + 3{{\rm{x}}^2}.$
c. $y = \frac{1}{3}{x^3} + 2{x^2} + 4x.$
a. Tập xác định: $D = R.$
Chiều biến thiên:
Ta có: $y’ = – 3{{\rm{x}}^2} + 6{\rm{x}}$ $ = – 3x\left( {x – 2} \right).$
$y’ = 0$ $ \Leftrightarrow – 3{\rm{x}}\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$
Hàm số nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right)$.
Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 0.$
Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = -4.$
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$
Bảng biến thiên:
Đồ thị:
Cho $x = – 1 \Rightarrow y = 0$, $x = 3 \Rightarrow y = -4.$
b. Tập xác định: $D = R.$
Chiều biến thiên:
Ta có: $y’ = – 3{{\rm{x}}^2} + 6{\rm{x}} = – 3x\left( {x – 2} \right).$
$y’ = 0 \Leftrightarrow – 3{\rm{x}}\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$
Hàm số nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right).$
Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 4.$
Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = 0.$
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$
Bảng biến thiên:
Đồ thị:
Cho $x = – 1 \Rightarrow y = 4$, $x = 3 \Rightarrow y = 0$.
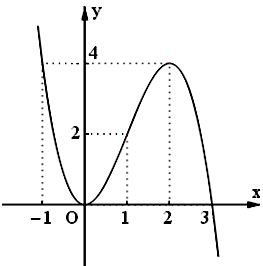
c. Tập xác định: $D = R.$
Chiều biến thiên:
Ta có: $y’ = {{\rm{x}}^2} + 4{\rm{x}} + 4$ $ = {\left( {x + 2} \right)^2} \ge 0$ $\forall x \in R.$
Hàm số đồng biến trên khoảng $\left( { – \infty ; + \infty } \right)$, hàm số không có cực trị.
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$
Bảng biến thiên:
Đồ thị: Cho $x = 0 \Rightarrow y = 0.$
Ví dụ 2. Cho hàm số $y = – {x^3} + 3{x^2} + 1$ có đồ thị $(C).$
a. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.
b. Viết phương trình tiếp tuyến của đồ thị $(C)$ tại $A\left( {3;1} \right).$
a. Khảo sát sự biến thiên và vẽ đồ thị:
Tập xác định: $D = R.$
Chiều biến thiên:
Ta có: $y’ = – 3{x^2} + 6x = – 3x\left( {x – 2} \right).$
$y’ = 0 \Leftrightarrow – 3x\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$
$y’ > 0 \Leftrightarrow x \in \left( {0 ; 2} \right)$, $y’ < 0$ $ \Leftrightarrow x \in \left( { – \infty ; 0} \right) \cup \left( {2 ; + \infty } \right).$
Hàm số nghịch biến trên mỗi khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right).$
Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 5.$
Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = 1.$
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$
Bảng biến thiên:
Đồ thị:
b. Phương trình tiếp tuyến của $(C)$ tại điểm $A\left( {3;1} \right)$ có dạng:
$y – 1 = y’\left( 3 \right).\left( {x – 3} \right)$ $ \Leftrightarrow y = – 9\left( {x – 3} \right) + 1$ $ \Leftrightarrow y = – 9x + 28.$
Ví dụ 3. Cho hàm số $y = {x^3} + 3{{\rm{x}}^2} – mx – 4$, trong đó $m$ là tham số.
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho với $m = 0$.
b. Với giá trị nào của $m$ thì hàm số nghịch biến trên khoảng $\left( { – \infty ;0} \right)$.
a. Khi $m = 0$ thì hàm số là: $y = {x^3} + 3{{\rm{x}}^2} – 4.$
Tập xác định: $D = R.$
Chiều biến thiên:
Ta có: $y’ = 3{{\rm{x}}^2} + 6{\rm{x}} = 3{\rm{x}}\left( {x + 2} \right).$
$y’ = 0 \Leftrightarrow 3{\rm{x}}\left( {x + 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = – 2.$
Hàm số đồng biến trên các khoảng $\left( { – \infty ; – 2} \right)$ và $\left( {0; + \infty } \right)$, nghịch biến trên khoảng $\left( { – 2;0} \right).$
Hàm số đạt cực đại tại điểm $x = – 2$, giá trị cực đại của hàm số là $y\left( { – 2} \right) = 0.$
Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = – 4.$
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$
Bảng biến thiên:
Đồ thị:
Cho $x = – 3 \Rightarrow y = – 4$, $x = 1 \Rightarrow y = 0.$
b. Hàm số $y = {x^3} + 3{{\rm{x}}^2} – mx – 4$ đồng biến trên khoảng $\left( { – \infty ;0} \right).$
$ \Leftrightarrow y’ = 3{{\rm{x}}^2} + 6{\rm{x}} – m \ge 0$, $\forall x \in \left( { – \infty ; 0} \right).$
Xét: $g\left( x \right) = 3{{\rm{x}}^2} + 6{\rm{x}} – m$, $x \in \left( { – \infty ; 0} \right).$
$g’\left( x \right) = 6{\rm{x}} + 6$ $ \Rightarrow g’\left( x \right) = 0 \Leftrightarrow x = – 1.$
Bảng biến thiên:
Nhìn vào bảng biến thiên ta thấy:
$y’ = g\left( x \right) = 3{{\rm{x}}^2} + 6{\rm{x}} – m \ge 0$, $\forall x \in \left( { – \infty ; 0} \right)$ $ \Leftrightarrow – 3 – m \ge 0 \Leftrightarrow m \le – 3.$
Vậy khi $m \le – 3$ thì yêu cầu của bài toán được thỏa mãn.
Ví dụ 4. Cho hàm số $y = 2{x^3} – 9{x^2} + 12x – 4$ có đồ thị $(C).$
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
b. Tìm $m$ để phương trình sau có $6$ nghiệm phân biệt: $2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m.$
a. Bảng biến thiên:
Đồ thị:
b. Ta có:
$2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m$ $ \Leftrightarrow 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4$ $ = m – 4.$
Gọi $\left( C \right):y = 2{x^3} – 9{x^2} + 12x – 4$ và $\left( {C’} \right):y = 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4.$
Ta thấy khi $x \ge 0$ thì: $\left( {C’} \right):y = 2{x^3} – 9{x^2} + 12x – 4.$
Mặt khác hàm số của đồ thị $(C’)$ là hàm số chẵn nên $(C’)$ nhận $Oy$ là trục đối xứng. Từ đồ thị $(C)$ ta suy ra đồ thị $(C’)$ như sau:
+ Giữ nguyên phần đồ thị $(C)$ bên phải trục $Oy$, ta được $\left( {{{C’}_1}} \right).$
+ Lấy đối xứng qua trục $Oy$ phần $\left( {{{C’}_1}} \right)$, ta được $\left( {{{C’}_2}} \right).$
+ $\left( {C’} \right) = \left( {{{C’}_1}} \right) \cup \left( {{{C’}_2}} \right).$
Số nghiệm của phương trình: $2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m$ $ \Leftrightarrow 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4 = m – 4$ là số giao điểm của đồ thị $(C’)$ và đường thẳng $\left( d \right):y = m – 4.$
Từ đồ thị $(C’)$, ta thấy yêu cầu bài toán: $ \Leftrightarrow 0 < m – 4 < 1$ $ \Leftrightarrow 4 < m < 5.$
Nguồn: toanmath.com
