Ôn tập chương IV
Bài tập vận dụng!1. Khái niệm số phức
+) Tập hợp số phức: $\mathbb{C}$
+) Số phức (dạng đại số) : $z = a + bi$ ($a,b \in \mathbb{R},a$ là phần thực, $b$ là phần ảo, $i$ là đơn vị ảo, ${i^2} = -1$)
+) $z$ là số thực $ \Leftrightarrow $ phần ảo của $z$ bằng $0\left( {b = 0} \right)$
+) $z$ là thuần ảo \( \Leftrightarrow \) phần thực của $z$ bằng $0\left( {a = 0} \right)$
Số $0$ vừa là số thực vừa là số ảo.
+) Hai số phức bằng nhau: $a + bi = a' + b'i \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right., (a,b,a',b' \in R)$
Chú ý: \({i^{4k}} = 1;\,\,\,{i^{4k + 1}} = i;\,\,\,\,{i^{4k + 2}} = - 1;\,\,\,\,{i^{4k + 3}} = - i\)
2. Biểu diễn hình học
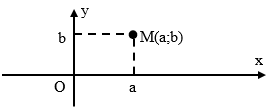
Số phức $z = a + bi\left( {a,b \in \mathbb{R}} \right)$ được biểu diễn bởi điểm $M\left( {a;b} \right)$ hay bởi $\overrightarrow u = (a;\;b)$ trong $mp\left( {Oxy} \right)$ (mp phức)
3. Cộng và trừ số phức
+) $\left( {a + bi} \right) + \left( {a' + b'i} \right) = \left( {a + a'} \right) + \left( {b + b'} \right)i$
+) $\left( {a + bi} \right) - \left( {a' + b'i} \right) = \left( {a - a'} \right) + \left( {b - b'} \right)i$
+) Số đối của $z = a + bi$ là $ - z = - a - bi$
+) $\vec u$ biểu diễn $z,\overrightarrow {u'} $ biểu diễn $z'$ thì $\overrightarrow u + \overrightarrow {u'} $ biểu diễn $z + z'$ và $\overrightarrow u - \overrightarrow {u'} $ biểu diễn $z - z'$
4. Nhân hai số phức
+) $\left( {a + bi} \right)\left( {a' + b'i} \right) = \;\left( {aa'-bb'} \right) + \left( {ab' + ba'} \right)i$
+) \(k(a + bi) = ka + kbi\,\,(k \in R)\)
5. Số phức liên hợp
Số phức liên hợp của số phức $z = a + bi$ là $\bar z = a - bi$
+) $\overline {\overline z } = z\;;\overline {z \pm z'} = \overline z \pm \overline {z'} \;;$ $\overline {z.z'} = \overline z .\overline {z'} ;\overline {\left( {\dfrac{{{z_1}}}{{{z_2}}}} \right)} = \dfrac{{{{\bar z}_1}}}{{{{\bar z}_2}}};z.\bar z = {a^2} + {b^2}$
+) $z$ là số thực $ \Leftrightarrow z = \overline z $; $z$ là số ảo $ \Leftrightarrow z = - \overline z $
6. Môđun của số phức
Cho $z = a + bi$
+) $\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt {z\bar z} = \left| {\overrightarrow {OM} } \right|$
+) $\left| z \right| \ge 0,\;\forall z \in C, \left| z \right| = 0 \Leftrightarrow z = 0$
+) $\left| {z.z'} \right| = \left| z \right|.\left| {z'} \right|$
+) \(\left| {\dfrac{z}{{z'}}} \right| = \dfrac{{\left| z \right|}}{{\left| {z'} \right|}}\)
+) $\left| {\left| z \right| - \left| {z'} \right|} \right| \le \left| {z \pm z'} \right| \le \left| z \right| + \left| {z'} \right|$
7. Chia hai số phức
+) Chia hai số phức: $\dfrac{{{{a + bi}}}}{{{{a' + b'i}}}} = \dfrac{{{{aa' - bb'}}}}{{a{'^2} + b{'^2}}} + \dfrac{{ab' + a'b}}{{a{'^2} + b{'^2}}}i$
+) ${z^{ - 1}} = \dfrac{1}{{{{\left| z \right|}^2}}}\bar z,(z \ne 0)$
+) $\dfrac{{z'}}{z} = z'{z^{ - 1}} = \dfrac{{z'.\bar z}}{{{{\left| z \right|}^2}}} = \dfrac{{z'.\bar z}}{{z.\bar z}}$
+) $\dfrac{{z'}}{z} = w \Leftrightarrow z' = wz$
8. Căn bậc hai của số phức
+) $z = x + yi$ là căn bậc hai của số phức \(w = a + bi\) $ \Leftrightarrow {z^2} = w$ $ \Leftrightarrow \left\{ \begin{array}{c}{x^2} - {y^2} = a\\2xy = b\end{array} \right.$
+) $w = 0$ có đúng $1$ căn bậc hai là $z{\rm{ }} = {\rm{ }}0$
+) $w \ne 0$ có đúng hai căn bậc hai đối nhau
+) Hai căn bậc hai của số thực $a > 0$ là $ \pm \sqrt a $
+) Hai căn bậc hai của số thực $a < 0$ là $ \pm \sqrt { - a} .i$
9. Phương trình bậc hai với hệ số phức
Cho phương trình $A{z^2} + Bz + C = 0{\rm{ }}\left( * \right)$($A,B,C$ là các số phức cho trước, $A \ne 0$)
$\Delta = {B^2} - 4AC$
+) $\Delta \ne 0$: $\left( * \right)$ có hai nghiệm phân biệt ${z_{1,2}} = \dfrac{{ - B \pm \delta }}{{2A}}$, ($\delta $ là $1$ căn bậc hai của $\Delta $)
+) $\Delta = 0$: $\left( * \right)$ có $1$ nghiệm kép: ${z_1} = {z_2} = - \dfrac{B}{{2A}}$
Chú ý: Nếu ${z_0} \in \mathbb{C}$ là một nghiệm của $\left( * \right)$ thì \(\overline {{z_0}} \) cũng là một nghiệm của $\left( * \right)$
10. Dạng lượng giác của số phức (dành cho chương trình nâng cao)
a) Acgumen của số phức ${\bf{z}} \ne {\bf{0}}$
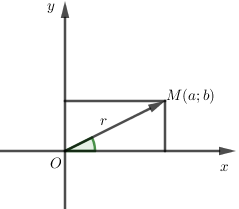
Cho số phức $z \ne 0.$ Gọi $M$ là điểm biểu diễn số $z.$ Số đo (radian) của mỗi góc lượng giác tia đầu $Ox,$ tia cuối $OM$ được gọi là một acgumen của $z.$ Nếu $\varphi $ là một acgumen của $z$ thì mọi acgumen của $z$ có dạng $\varphi + {\rm{ }}k2\pi \left( {k \in \mathbb{Z}} \right)$
b) Dạng lượng giác của số phức
Dạng $z = r\left( {\cos \varphi + {\rm{ }}i\sin \varphi } \right)\;\left( {r > 0} \right)$ là dạng lượng giác của $z = a + bi\left( {a,b \in R} \right)\left( {z \ne 0} \right)$
\( \Leftrightarrow \left\{ \begin{array}{l}r = \sqrt {{a^2} + {b^2}} \\c{\rm{os}}\varphi = \dfrac{a}{r}\\\sin \varphi = \dfrac{b}{r}\end{array} \right.\) ($\varphi $ là acgumen của $z,\varphi = \left( {Ox,OM} \right)$)
c) Nhân, chia số phức dưới dạng lượng giác
Nếu $z = r\left( {\cos \varphi + {\rm{ }}i\sin \varphi } \right),$$\;z' = {\rm{ }}r'\left( {\cos \varphi '{\rm{ }} + {\rm{ }}i\sin \varphi '} \right)$ thì:
$z.z' = {\rm{ }}rr'\left[ {\cos (\varphi + \varphi '){\rm{ }} + {\rm{ }}i\sin (\varphi + \varphi ')} \right]$
\(\dfrac{{z}}{{{z'}}} = \dfrac{r}{{r'}}\left[ {c{\rm{os}}(\varphi - \varphi ') + {\rm{i}}\sin (\varphi - \varphi ')} \right]\).
d) Công thức Moa-vrơ
Với $n$ là số nguyên, $n \ge 1$ thì: \({\left[ {r(c{\rm{os}}\varphi + {\rm{i}}\sin \varphi )} \right]^n} = {r^n}(\cos n\varphi + {\rm{i}}\sin n\varphi )\)
Khi $r = 1,$ ta được : \({(c{\rm{os}}\varphi + {\rm{i}}\sin \varphi )^n} = (\cos n\varphi + {\rm{i}}\sin n\varphi )\)
e) Căn bậc hai của số phức dưới dạng lượng giác
Các căn bậc hai của số phức $z{\rm{ }} = {\rm{ }}r(\cos \varphi + {\rm{ }}i\sin \varphi )\;\;\left( {r > 0} \right)$ là : \(\sqrt r \left( {c{\rm{os}}\dfrac{\varphi }{2} + {\rm{i}}\sin \dfrac{\varphi }{2}} \right)\) và \( - \sqrt r \left( {c{\rm{os}}\dfrac{\varphi }{2} + {\rm{i}}\sin \dfrac{\varphi }{2}} \right) = \sqrt r \left[ {c{\rm{os}}\left( {\dfrac{\varphi }{2} + \pi } \right) + {\rm{i}}\sin \left( {\dfrac{\varphi }{2} + \pi } \right)} \right]\)
Nguồn: vungoi
