Viết phương trình tổng quát của đường thẳng (Oxy)

Để viết phương trình tổng quát của đường thẳng $\Delta$ ta cần xác định:
+ Điểm $A(x_0;y_0)\in \mathrm{\Delta }$.
+ Một vectơ pháp tuyến $\overrightarrow{n}\left(a;b\right)$ của $\Delta .$
Khi đó phương trình tổng quát của $\Delta$ là $a\left(x–x_0\right)+b\left(y–y_0\right)=0$.
Chú ý:
a. Đường thẳng $\Delta$ có phương trình tổng quát là: $ax+by+c=0$, $a^2+b^2\ne 0$ nhận $\overrightarrow{n}\left(a;b\right)$ làm vectơ pháp tuyến.
b. Nếu hai đường thẳng song song với nhau thì VTPT đường thẳng này cũng là VTPT của đường thẳng kia.
c. Phương trình đường thẳng $\Delta$ qua điểm $M\left(x_0;y_0\right)$ có dạng $\Delta$: $a\left(x–x_0\right)+b\left(y–y_0\right)=0$ với $a^2+b^2\ne 0$. Đặc biệt:
+ Nếu đường thẳng $\Delta$ song song với trục $Oy:$ $\Delta :$ $x=x_0$.
+ Nếu đường thẳng $\Delta$ cắt trục $Oy:$ $\Delta :$ $y–y_0=k\left(x–x_0\right)$.
d. Phương trình đường thẳng đi qua $A\left(a;0\right),B\left(0;b\right)$ với $ab\ne 0$ có dạng $\frac{x}{a}+\frac{y}{b}=1$.
Ví dụ 1: Cho tam giác $ABC$ biết $A\left(2;0\right),B\left(0;4\right),C(1;3)$. Viết phương trình tổng quát của:
a. Đường cao $AH$.
b. Đường trung trực của đoạn thẳng $BC$.
c. Đường thẳng $AB$.
d. Đường thẳng qua $C$ và song song với đường thẳng $AB$.

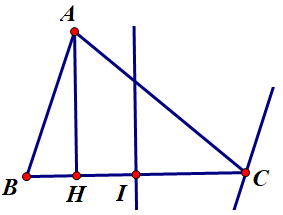
a. Vì $AH\mathrm{\perp }BC$ nên $\overrightarrow{BC}$ là vectơ pháp tuyến của $AH.$
Ta có $\overrightarrow{BC}\left(1;–1\right)$ suy ra đường cao $AH$ đi qua $A$ và nhận $\overrightarrow{BC}$ là vectơ pháp tuyến có phương trình tổng quát là $1.\left(x–2\right)–1.\left(y–0\right)=0$ hay $x–y–2=0$.
b. Đường trung trực của đoạn thẳng $BC$ đi qua trung điểm $BC$ và nhận vectơ $\overrightarrow{BC}$ làm vectơ pháp tuyến.
Gọi $I$ là trung điểm $BC$ khi đó $x_I=\frac{x_B+x_C}{2}=\frac{1}{2}$, $y_I=\frac{y_B+y_C}{2}=\frac{7}{2}$ $\Rightarrow I\left(\frac{1}{2};\frac{7}{2}\right)$.
Suy ra phương trình tổng quát của đường trung trực $BC$ là:
$1.\left(x–\frac{1}{2}\right)–1.\left(y–\frac{7}{2}\right)=0$ hay $x–y+3=0$.
c. Phương trình tổng quát của đường thẳng $AB$ có dạng $\frac{x}{2}+\frac{y}{4}=1$ hay $2x+y–4=0$.
d. Giải bằng 2 cách sau:
Cách 1: Đường thẳng $AB$ có VTPT là $\overrightarrow{n}\left(2;1\right)$ do đó vì đường thẳng cần tìm song song với đường thẳng $AB$ nên nhận $\overrightarrow{n}\left(2;1\right)$ làm VTPT do đó có phương trình tổng quát là $2.\left(x–1\right)+1.\left(y–3\right)=0$ hay $2x+y–5=0$.
Cách 2: Đường thẳng $\Delta$ song song với đường thẳng $AB$ có dạng $2x+y+c=0$.
Điểm $C$ thuộc $\Delta$ suy ra $2.1+3+c=0$ $\Rightarrow c=–5$.
Vậy đường thẳng cần tìm có phương trình tổng quát là $2x+y–5=0$.
Ví dụ 2: Cho đường thẳng $d:x–2y+3=0$ và điểm $M\left(–1;2\right)$. Viết phương trình tổng quát của đường thẳng $\Delta$ biết:
a. $\Delta$ đi qua điểm $M$ và có hệ số góc $k=3$.
b. $\Delta$ đi qua $M$ và vuông góc với đường thẳng $d$.
c. $\Delta$ đối xứng với đường thẳng $d$ qua $M$.
a. Đường thẳng $\Delta$ có hệ số góc $k=3$ có phương trình dạng $y=3x+m$.
Mặt khác $M\in \mathrm{\Delta }$ $\Rightarrow 2=3.\left(–1\right)+m$ $\Rightarrow m=5$.
Suy ra phương trình tổng quát đường thẳng $\Delta$ là $y=3x+5$ hay $3x–y+5=0$.
b. Ta có $x–2y+3=0$ $\iff y=\frac{1}{2}x+\frac{3}{2}$ do đó hệ số góc của đường thẳng $d$ là $k_d=\frac{1}{2}$.
Vì $\mathrm{\Delta }\mathrm{\perp }d$ nên hệ số góc của $\Delta$ là $k_{\mathrm{\Delta }}$ thì $k_d.k_{\mathrm{\Delta }}=–1\Rightarrow k_{\mathrm{\Delta }}=–2$.
Do đó $\mathrm{\Delta }:y=–2x+m$, $M\in \mathrm{\Delta }$ $\Rightarrow 2=–2.(–1)+m$ $\Rightarrow m=–2$.
Suy ra phương trình tổng quát đường thẳng $\mathrm{\Delta }$ là $y=–2x–2$ hay $2x+y+2=0$.
c. Giải bằng 2 cách sau:
Cách 1: Ta có $–1–2.2+3\ne 0$ do đó $M\notin d$ vì vậy đường thẳng $\Delta$ đối xứng với đường thẳng $d$ qua $M$ sẽ song song với đường thẳng $d$ suy ra đường thẳng $\Delta$ có VTPT là $\overrightarrow{n}\left(1;–2\right)$.
Ta có $A\left(1;2\right)\in d$, gọi $A^{\prime }$ đối xứng với $A$ qua $M$ khi đó $A^{\prime }\in \mathrm{\Delta }$.
Ta có $M$ là trung điểm của $A{A}^{\prime }$.
$\Rightarrow \{\begin{array}{c}{x}_M=\frac{x_A+x_{A^{\prime }}}{2}\\ y_M=\frac{y_A+y_{A^{\prime }}}{2}\end{array}$ $\Rightarrow \{\begin{array}{c}{x}_{A^{\prime }}=2x_M–x_A=–3\\ y_{A^{\prime }}=2y_M–y_A=2\end{array}$ $\Rightarrow A^{\prime }\left(–3;2\right)$.
Vậy phương trình tổng quát đường thẳng $\Delta$ là $1.\left(x+3\right)–2\left(y–2\right)=0$ hay $x–2y+7=0$.
Cách 2: Gọi $A\left(x_0;y_0\right)$ là điểm bất kỳ thuộc đường thẳng $d$, $A^{\prime }\left(x;y\right)$ là điểm đối xứng với $A$ qua $M$.
Khi đó $M$ là trung điểm của $A{A}^{\prime }$, suy ra:
$\{\begin{array}{c}{x}_M=\frac{x_0+x}{2}\\ y_M=\frac{y_0+y}{2}\end{array}$ $\iff \{\begin{array}{c}–1=\frac{x_0+x}{2}\\ 2=\frac{y_0+y}{2}\end{array}$ $\iff \{\begin{array}{c}{x}_0=–2–x\\ y_0=4–y\end{array}$
Ta có $A\in d$ $\Rightarrow x_0–2y_0+3=0$, suy ra:
$\left(–2–x\right)–2.\left(4–y\right)+3=0$ $\iff x–2y+7=0$.
Vậy phương trình tổng quát của $\Delta$ đối xứng với đường thẳng $d$ qua $M$ là $x–2y+7=0$.
Ví dụ 3: Biết hai cạnh của một hình bình hành có phương trình $x–y=0$ và $x+3y–8=0$, tọa độ một đỉnh của hình bình hành là $\left(–2;2\right)$. Viết phương trình các cạnh còn lại của hình bình hành.
Đặt tên hình bình hành là $ABCD$ với $A\left(–2;2\right)$, do tọa độ điểm $A$ không là nghiệm của hai phương trình đường thẳng trên nên ta giả sử $BC:x–y=0$, $CD:x+3y–8=0$.
Vì $AB\parallel CD$ nên cạnh $AB$ nhận $\overrightarrow{n_{CD}}\left(1;3\right)$ làm VTPT do đó có phương trình là $1.\left(x+2\right)+3.\left(y–2\right)=0$ hay $x+3y–4=0$.
Tương tự cạnh $AD$ nhận $\overrightarrow{n_{BC}}\left(1;–1\right)$ làm VTPT do đó có phương trình là $1.\left(x+2\right)–1.\left(y–2\right)=0$ hay $x–y+4=0$.
Ví dụ 4: Cho điểm $M\left(1;4\right)$. Viết phương trình đường thẳng qua $M$ lần lượt cắt hai tia $Ox$, tia $Oy$ tại $A$ và $B$ sao cho tam giác $OAB$ có diện tích nhỏ nhất.
Giả sử $A\left(a;0\right),B\left(0;b\right)$ với $a>0,b>0$. Khi đó đường thẳng đi qua $A,B$ có dạng $\frac{x}{a}+\frac{y}{b}=1$. Do $M\in AB$ nên $\frac{1}{a}+\frac{4}{b}=1$.
Mặt khác $S_{OAB}=\frac{1}{2}OA.OB=\frac{1}{2}ab$.
Áp dụng BĐT Côsi, ta có: $1=\frac{1}{a}+\frac{4}{b}\ge 2\sqrt{\frac{4}{ab}}$ $\Rightarrow ab\ge 16\Rightarrow S_{OAB}\ge 8$.
Suy ra $S_{OAB}$ nhỏ nhất khi $\frac{1}{a}=\frac{4}{b}$ và $\frac{1}{a}+\frac{4}{b}=1$ do đó $a=2;b=8$.
Vậy phương trình đường thẳng cần tìm là $\frac{x}{2}+\frac{y}{8}=1$ hay $4x+y–8=0$.