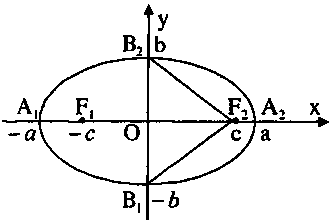
1. Định nghĩa
Cho hai điểm cố định \({F_1}\) và \({F_2}\) với \({F_1}{F_2} = 2c\) \((c > 0).\)
Đường elip (còn gọi là elip) là tập hợp các điểm \(M\) sao cho \(M{F_1} + M{F_2} = 2a\) trong đó \(a\) là một số không đổi lớn hơn \(c.\)
Hai điểm \({F_1}\) và \({F_2}\) gọi là các tiêu điểm của elip.
Khoảng cách \(2c\) giữa hai tiêu điểm gọi là tiêu cự của elip.
Nếu điểm \(M\) nằm trên elip thì các khoảng cách \(M{F_1}\) và \(M{F_2}\) gọi là các bán kính qua tiêu điểm của điểm \(M.\)
Trung điểm \(I\) của đoạn thẳng \({F_1}{F_2}\) gọi là tâm của elip.
2. Phương trình chính tắc của đường elip
Xét elip gồm những điểm \(M\) sao cho \(M{F_1} + M{F_2} = 2a\) trong đó \({F_1}{F_2} = 2c.\)
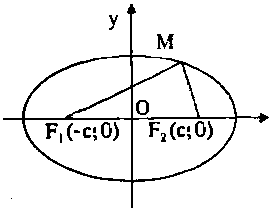
Ta chọn hệ trục toạ độ sao cho các tiêu điểm có toạ độ \({F_1} = ( – c;0)\), \({F_2} = (c;0).\) Khi đó elip có phương trình là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({b^2} = {a^2} – {c^2}\) \((1).\)
Phương trình \((1)\) gọi là phương trình chính tắc của elip.
Chú ý:
1) Trong phương trình chính tắc: \(a > b > 0\), tiêu điểm thuộc trục hoành.
2) Công thức bán kính qua tiêu điểm:
\(M{F_1} = a + \frac{{cx}}{a} = a + ex\) và \(M{F_2} = a – \frac{{cx}}{a} = a – ex.\)
(không vuông góc với trục tung, nhưng bán kính qua tiêu điểm biểu diễn được qua một biến duy nhất là \(x\)).
3) Cũng là elip trên, nhưng nếu chọn hệ trục toạ độ sao cho các tiêu điểm có toạ độ \({F_1} = (0; – c)\) và \({F_2} = (0;c)\), khi đó elip có phương trình là:
\(\frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\) với \({b^2} = {a^2} – {c^2}\) \((2).\)
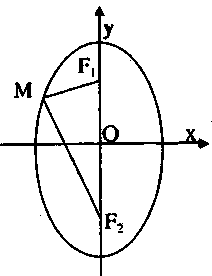
Trong trường hợp này tiêu điểm thuộc trục tung và phương trình \((2)\) không được gọi là phương trình chính tắc của elip.
3. Hình dạng của elip
a) Tính đối xứng
Xét các phương trình \((1)\) và \((2).\) Đó là các phương trình chẵn đối với \(x\) và \(y\) nên elip có trục đối xứng là các đường thẳng \(Ox\) và \(Oy\), do đó nó nhận gốc toạ độ \(O\) làm tâm đối xứng.
b) Hình chữ nhật cơ sở
Xét elip có phương trình chính tắc \((1).\)
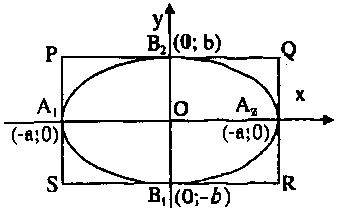
Rõ ràng elip cắt trục \(Ox\) tại hai điểm \({A_1}( – a;0)\) và \({A_2}(a;0)\), cắt trục \(Oy\) tại hai điểm \({B_1}(0; – b)\) và \({B_2}(0;b).\) Bốn điểm ấy được gọi là bốn đỉnh của elip. Đoạn thẳng \({A_1}{A_2}\) gọi là trục lớn, đoạn thẳng \({B_1}{B_2}\) gọi là trục bé của elip.
Rõ ràng \({A_1}{A_2} = 2a\), \({B_1}{B_2} = 2c.\)
Vẽ các đường thẳng \(y = \pm a\), \(y = \pm b.\) Bốn đường thẳng đó tạo thành một hình chữ nhật \(PQRS.\) Ta gọi đó là hình chữ nhật cơ sở của elip.
Chú ý:
Từ \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \( \Rightarrow \left\{ {\frac{{{x^2}}}{{{a^2}}} \le 1{\rm{\:và\:}}\frac{{{y^2}}}{{{b^2}}} \le 1} \right\}\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{ – a \le x \le a}\\
{ – b \le x \le b}
\end{array}} \right..\)
Bởi vậy mọi điểm của elip đều thuộc miền chữ nhật cơ sở của nó.
Tiêu điểm của elip nằm trên trục lớn.
c) Tâm sai của elip
Tỉ số giữa tiêu cự và độ dài trục lớn gọi là tâm sai của elip và ký hiệu là \(e.\) Vậy \(e = \frac{c}{a}.\)
Rõ ràng \(0 < e < 1\). Do \({c^2} = {a^2} – {b^2}\) và \(a\) không đổi suy ra:
+ Nếu \(e\) càng bé (càng gần tới \(0\)) thì \(b\) càng gần \(a\), hình chữ nhật cơ sở càng gần với hình vuông, do đó hình elip càng “béo (càng gần với hình tròn).
+ Nếu \(e\) càng lớn (càng gần tới \(1\)) thì \(b\) càng gần tới \(0\), hình chữ nhật cơ sở càng “dẹt”, do đó hình elip càng “gầy” (càng “dẹt”).
4. Đường chuẩn của elip
1. Định nghĩa
Cho elip có phương trình chính tắc:
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)
Các đường thẳng \(\left( {{\Delta _1}} \right):x = – \frac{a}{e}\), \(\left( {{\Delta _2}} \right):x = \frac{a}{e}\) được gọi là các đường chuẩn của elip.
\(\left( {{\Delta _1}} \right)\) gọi là đường chuẩn ứng với tiêu điểm \({F_1}.\)
\(\left( {{\Delta _2}} \right)\) gọi là đường chuẩn ứng với tiêu điểm \({F_2}.\)

2. Định lý
Tỉ số giữa khoảng cách từ một điểm bất kì trên elip đến một tiêu điểm và đường chuẩn tương ứng bằng tâm sai của elip.
\(\frac{{M{F_i}}}{{d\left( {M,\left( {{\Delta _i}} \right)} \right)}} = e\) \((i = 1;2).\)
Để ý \(\frac{a}{e} = \frac{{{a^2}}}{c} > \frac{{{a^2}}}{a} = a\) tức là \(\frac{a}{e} > a\) và \( – \frac{a}{e} < a\), suy ra các đường chuẩn không cắt elip.
II. CÁC BÀI TOÁN VÀ THÍ DỤ
Bài toán 1. Xác định các yếu tố của elip.
Thí dụ 1: Cho các đường cong: \(\left( {{E_1}} \right):{x^2} + 25{y^2} = 25\), \(\left( {{E_2}} \right):49{x^2} + 64{y^2} = 1\), \(\left( {{E_3}} \right):9{x^2} + 4{y^2} = 1.\) Đặt tên cho các đường cong nói trên. Nếu là elip hãy xác định trục lớn, trục bé và toạ độ tiêu điểm của nó.
+ Xét đường cong \(\left( {{E_1}} \right):{x^2} + 25{y^2} = 25\) \((1).\)
Ta có \((1) \Leftrightarrow \frac{{{x^2}}}{{25}} + {y^2} = 1.\) Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = 5\), \(b = 1\) \( \Rightarrow \) \(\left( {{E_1}} \right)\) là đường elip.
Trục lớn: \(2a = 10\), trục bé: \(2b = 2.\)
Tiêu điểm \(c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {25 – 1} = 2\sqrt 6 .\)
Suy ra hai tiêu điểm là \({F_1}( – 2\sqrt 6 ;0)\), \({F_2}(2\sqrt 6 ;0).\)
+ Xét đường cong \(\left( {{E_2}} \right):49{x^2} + 64{y^2} = 1\) \((2).\)
Ta có \((2) \Leftrightarrow \frac{{{x^2}}}{{\frac{1}{{49}}}} + \frac{{{y^2}}}{{\frac{1}{{64}}}} = 1.\) Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = \frac{1}{7}\), \(b = \frac{1}{8}\) \( \Rightarrow \left( {{E_2}} \right)\) là đường elip.
Trục lớn: \(2a = \frac{2}{7}\), trục bé: \(2b = \frac{1}{4}.\)
Tiêu điểm \(c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {\frac{1}{{49}} – \frac{1}{{64}}} \) \( = \sqrt {\frac{{15}}{{49.64}}} = \frac{{\sqrt {15} }}{{56}}.\)
Suy ra hai tiêu điểm là \({F_1}\left( { – \frac{{\sqrt {15} }}{{56}};0} \right)\), \({F_2}\left( {\frac{{\sqrt {15} }}{{56}};0} \right).\)
+ Xét đường cong \(\left( {{E_3}} \right):9{x^2} + 4{y^2} = 1\) \((3).\)
Ta có \((3) \Leftrightarrow \frac{{{x^2}}}{{\frac{1}{9}}} + \frac{{{y^2}}}{{\frac{1}{4}}} = 1.\) Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = \frac{1}{3}\), \(b = \frac{1}{2}\), \(0 < a < b\) \( \Rightarrow ({E_3})\) là đường elip.
Trục bé \(2a = \frac{2}{3}\), trục lớn: \(2b = 1.\)
Tiêu điểm \(c = \sqrt {{b^2} – {a^2}} \) \( = \sqrt {\frac{1}{4} – \frac{1}{9}} = \frac{{\sqrt 5 }}{6}.\)
Suy ra hai tiêu điểm là \({F_1}\left( {0; – \frac{{\sqrt 5 }}{6}} \right)\), \({F_2}\left( {0;\frac{{\sqrt 5 }}{6}} \right).\)
Thí dụ 2: Cho các đường cong \(\left( {{E_1}} \right):4{x^2} + 9{y^2} = 36\), \(\left( {{E_2}} \right):(2 – \sqrt 3 ){x^2} + {y^2} = 2 + \sqrt 3 .\) Đặt tên cho các đường cong nói trên. Tìm tâm sai và viết phương trình các đường chuẩn nếu nó là elip.
+ Xét đường cong \(\left( {{E_1}} \right):4{x^2} + 9{y^2} = 36\) \((1).\)
Chia hai vế cho \(36\) ta có \((1) \Leftrightarrow \frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1.\) Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = 3\), \(b = 2\) \( \Rightarrow \left( {{E_1}} \right)\) là đường elip.
Do \(a > b\) \( \Rightarrow c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {9 – 4} = \sqrt 5 .\) Tâm sai: \(e = \frac{c}{a} = \frac{{\sqrt 5 }}{3}.\)
Phương trình các đường chuẩn là: \(x = \pm \frac{a}{e}\) \( = \pm \frac{{{a^2}}}{c} = \pm \frac{9}{{\sqrt 5 }}\) \( \Leftrightarrow x = \pm \frac{9}{{\sqrt 5 }}.\)
+ Xét đường cong \(\left( {{E_2}} \right):(2 – \sqrt 3 ){x^2} + {y^2} = 2 + \sqrt 3 \) \((2).\)
Nhân hai vế với \(2 + \sqrt 3 \) ta có: \((1) \Leftrightarrow {x^2} + (2 + \sqrt 3 ){y^2} = 1\) \( \Leftrightarrow {x^2} + \frac{{{y^2}}}{{2 – \sqrt 3 }} = 1.\)
Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = 1\), \(b = 2 – \sqrt 3 \) \( \Rightarrow \left( {{E_2}} \right)\) là đường elip.
Do \(a > b\) \( \Rightarrow c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {{1^2} – {{(2 – \sqrt 3 )}^2}} \) \( = \sqrt {4\sqrt 3 – 6} .\)
Tâm sai: \(e = \frac{c}{a}\) \( = \frac{{4\sqrt 3 – 6}}{1}\) \( = 4\sqrt 3 – 6.\)
Phương trình đường chuẩn là \(x = \pm \frac{a}{e}\) \( = \frac{1}{{4\sqrt 3 – 6}}\) \( = \frac{{2 + \sqrt 3 }}{6}.\)
Thí dụ 3: Cho điểm \(M\left( {2;\frac{{2\sqrt 5 }}{5}} \right)\) và elip \((E):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) \((1).\)
a) Tính các bán kính qua các tiêu điểm của elip kẻ từ \(M.\)
b) Một đường thẳng song song với \(Oy\) đi qua tiêu điểm của elip cắt elip tại hai điểm \(A\) và \(B\), tính độ dài đoạn thẳng \(AB.\)
a) Tính các bán kính qua các tiêu điểm.
Phương trình \((1)\) có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(\left\{ {\begin{array}{*{20}{l}}
{a = \sqrt 5 }\\
{b = 2}
\end{array}} \right.\) \( \Rightarrow c = \sqrt {{a^2} – {b^2}} .\)
\( \Rightarrow \sqrt {5 – 4} = 1\), \(e = \frac{c}{a} = \frac{1}{{\sqrt 5 }}.\)
Thay toạ độ điểm \(M\) vào phương trình \((1)\) ta có \(\frac{{{2^2}}}{5} + \frac{{{2^2}}}{{4.5}} = 1\) là đẳng thức đúng.
Suy ra \(M\) là một điểm nằm trên elip \((E).\)
Áp dụng công thức bán kính qua tiêu điểm ta có:
\(M{F_1} = a + \frac{c}{a}{x_M}\) \( = \sqrt 5 + \sqrt 5 .\frac{{2\sqrt 5 }}{5}\) \( = \sqrt 5 + 2.\)
\(M{F_2} = a – e{x_M}\) \( = \sqrt 5 – \sqrt 5 .\frac{{2\sqrt 5 }}{5} = \sqrt 5 – 2.\)
Tóm lại: \(M{F_1} = \sqrt 5 + 2\) và \(M{F_2} = \sqrt 5 – 2.\)
b) Tính độ dài đoạn thẳng \(AB.\)
Giả sử \(AB//Oy\) là dây cung qua \({F_1}( – 1;0)\) của elip.
Rõ ràng \({x_A} = {x_B} = – 1.\)
Ta có \(AB = 2A{F_1}\) \( = 2\left[ {\sqrt 5 – \sqrt 5 .( – 1)} \right]\) \( = 4\sqrt 5 .\)
Vậy \(AB = 4\sqrt 5 .\)
Thí dụ 4: Tìm trên elip \((E):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{1} = 1\) các điểm \(M\) trong mỗi trường hợp sau:
a) Nhìn hai tiêu điểm của nó dưới một góc vuông.
b) \(2M{F_1} = M{F_2}\) trong đó \({F_1}\), \({F_2}\) là các tiêu điểm của elip.
Phương trình của \((E)\) có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(\left\{ {\begin{array}{*{20}{l}}
{a = \sqrt 5 }\\
{b = 1}
\end{array}} \right.\) \( \Rightarrow c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {5 – 1} = 2\), \(e = \frac{c}{a} = \frac{2}{{\sqrt 5 }}.\)
Gọi \(M\left( {{x_0};{y_0}} \right)\) là một điểm trên elip \((E).\)
Ta có \(M{F_1} = a + e{x_0}\), \(M{F_2} = a – e{x_0}.\)

a) Điểm \(M\) nhìn các tiêu điểm của elip dưới một góc vuông \( \Leftrightarrow M{F_1} \bot M{F_2}\) \( \Leftrightarrow MF_1^2 + MF_2^2 = {\left( {{F_1}{F_2}} \right)^2}.\)
\( \Leftrightarrow {\left( {a + e{x_0}} \right)^2} + {\left( {a – e{x_0}} \right)^2} = {(2c)^2}\) \( \Leftrightarrow {a^2} + {\left( {e{x_0}} \right)^2} = 2{c^2}.\)
\( \Leftrightarrow 5 + {\left( {\frac{{2{x_0}}}{{\sqrt 5 }}} \right)^2} = {2.2^2}\) \( \Leftrightarrow x_0^2 = \frac{{15}}{4}\) \( \Leftrightarrow {x_0} = \pm \frac{{\sqrt {15} }}{2}.\)
Thay vào phương trình của \((E)\) có \(\frac{{15}}{{5.4}} + y_0^2 = 1\) \( \Leftrightarrow y_0^2 = \frac{3}{4}\) \( \Leftrightarrow {y_0} = \pm \frac{{\sqrt 3 }}{2}.\)
Vậy trên \((E)\) có bốn điểm \(M\) cùng nhìn hai tiêu điểm của nó dưới một góc vuông là:
\({M_1}\left( {\frac{{\sqrt {15} }}{2};\frac{{\sqrt 3 }}{2}} \right)\), \({M_2}\left( {\frac{{\sqrt {15} }}{2}; – \frac{{\sqrt 3 }}{2}} \right)\), \({M_3}\left( { – \frac{{\sqrt {15} }}{2};\frac{{\sqrt 3 }}{2}} \right)\), \({M_4}\left( { – \frac{{\sqrt {15} }}{2}; – \frac{{\sqrt 3 }}{2}} \right).\)
b) \(2M{F_1} = M{F_2}\) \( \Leftrightarrow 2\left( {a + e{x_0}} \right) = a – e{x_0}\) \( \Leftrightarrow 3e{x_0} = – a.\)
\( \Leftrightarrow {x_0} = – \frac{a}{{3e}} = – \frac{{{a^2}}}{{3c}} = – \frac{5}{6}.\)
Thay vào phương trình của \((E)\) có \(\frac{{{5^2}}}{{5.36}} + y_0^2 = 1.\)
\( \Leftrightarrow y_0^2 = \frac{{31}}{{36}}\) \( \Leftrightarrow {y_0} = \pm \frac{{\sqrt {31} }}{6}.\)
Vậy trên \((E)\) có hai điểm \(M\) thoả mãn \(2M{F_1} = M{F_2}\) là: \({M_1}\left( { – \frac{5}{6}; – \frac{{\sqrt {31} }}{6}} \right)\) và \({M_2}\left( { – \frac{5}{6};\frac{{\sqrt {31} }}{6}} \right).\)
Thí dụ 5: Tìm tâm sai của elip trong mỗi trường hợp sau đây:
a) Mỗi tiêu điểm nhìn trục nhỏ dưới một góc \(\alpha .\)
b) Khoảng cách giữa hai đỉnh trên hai trục bằng \(k\) lần tiêu cự \(\left( {k > \frac{1}{2}} \right).\)
c) Khoảng cách giữa hai đường chuẩn bằng \(k\) lần tiêu cự.
a) Theo giả thiết \(\tan \alpha = \frac{b}{c}.\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{b^2}}}{{{c^2}}}.\)
\( \Leftrightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{{b^2} + {c^2}}}{{{c^2}}}.\)
\( \Leftrightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{{a^2}}}{{{c^2}}}.\)
\( \Leftrightarrow \frac{c}{a} = \cos \alpha \) hay \(e = \cos \alpha .\)
b) Trong tam giác \({A_2}O{B_2}\) vuông tại \(O\) ta có \({\left( {{A_2}{B_2}} \right)^2} = OA_2^2 + OB_2^2\) \( = {a^2} + {b^2}.\)
Theo giả thiết ta có \({A_2}{B_2} = k{F_1}{F_2}\) \( \Leftrightarrow {\left( {{A_2}{B_2}} \right)^2} = {(k2c)^2}\) \( \Leftrightarrow {a^2} + {b^2} = 4{k^2}{c^2}.\)
\( \Leftrightarrow {a^2} + \left( {{a^2} – {c^2}} \right) = 4{k^2}{c^2}\) \( \Leftrightarrow 2{a^2} = \left( {4{k^2} + 1} \right){c^2}.\)
\( \Leftrightarrow \frac{{{c^2}}}{{{a^2}}} = \frac{2}{{4{k^2} + 1}}\) \( \Leftrightarrow e = \sqrt {\frac{2}{{4{k^2} + 1}}} .\)
c) Phương trình các đường chuẩn là \(x = \pm \frac{a}{e}\) suy ra khoảng cách giữa chúng là \(d = \frac{{2a}}{e}.\)
Theo giả thiết \(d = k{A_2}{B_2}\) \( \Leftrightarrow \frac{{2a}}{e} = k2c\) \( \Leftrightarrow \frac{1}{k} = \frac{c}{a}.e\) \( \Leftrightarrow {e^2} = \frac{1}{k}\) \( \Leftrightarrow e = – \frac{1}{{\sqrt k }}.\)
Bài toán 2. Viết phương trình của elip.
Thí dụ 6: Viết phương trình chính tắc của elip \((E)\) biết rằng \((E)\) có:
a) Độ dài trục lớn bằng \(6\), tiêu cự bằng \(4.\)
b) Một tiêu điểm \({F_1}( – 2;0)\) và độ dài trục lớn bằng \(10.\)
c) Một tiêu điểm \({F_1}( – \sqrt 3 ;0)\) và điểm \(M\left( {1;\frac{{\sqrt 3 }}{2}} \right)\) nằm trên \((E).\)
d) Đi qua hai điểm \(M(1;0)\) và \(N\left( {\frac{{\sqrt 3 }}{2};1} \right).\)
e) Tiêu cự bằng \(8\), tâm sai bằng \(\frac{4}{5}\) và tiêu điểm thuộc trục hoành.
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với \({b^2} = {a^2} – {c^2}\)) \((1).\)
a) Theo giả thiết \(\left\{ {\begin{array}{*{20}{l}}
{2a = 6}\\
{2c = 4}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 3}\\
{c = 2}
\end{array}} \right.\) \( \Rightarrow {a^2} – {c^2} = 5\) hay \({b^2} = 5.\)
Thay vào \((1)\) có: \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1.\)
Đó là phương trình chính tắc của elip cần tìm.
b) Theo giả thiết \(\left\{ {\begin{array}{*{20}{l}}
{{F_1}( – 2;0)}\\
{2a = 10}
\end{array}} \right.\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{c = – 2}\\
{a = 5}
\end{array}} \right.\) \( \Rightarrow {a^2} – {c^2} = 25 – 4 = 21\) hay \({b^2} = 21.\)
Thay vào \((1)\) có \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{21}} = 1.\)
Đó là phương trình chính tắc của elip cần tìm.
c) Tiêu điểm \({F_1}( – \sqrt 3 ;0)\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{c = \sqrt 3 }\\
{{b^2} = {a^2} – {c^2}}
\end{array}} \right.\) \( \Rightarrow {b^2} = {a^2} – 3\) \( \Leftrightarrow {a^2} = {b^2} + 3\) \((2).\)
Điểm \(M\left( {1;\frac{{\sqrt 3 }}{2}} \right)\) nằm trên \((E) \Leftrightarrow \frac{1}{{{a^2}}} + \frac{3}{{4{b^2}}} = 1\) \((3).\)
Thay \((2)\) vào \((3)\) ta có: \(\frac{1}{{{b^2} + 3}} + \frac{3}{{4{b^2}}} = 1\) \( \Leftrightarrow 4{b^2} + 3\left( {{b^2} + 3} \right) = 4{b^2}\left( {{b^2} + 3} \right).\)
\( \Leftrightarrow 4{\left( {{b^2}} \right)^2} + 5{b^2} – 9 = 0\) \( \Leftrightarrow {b^2} = 1.\)
Thay vào \((2)\) có \({a^2} = 4.\)
Với \({{a^2} = 4}\), \({{b^2} = 1}\) thay vào \((1)\) có: \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1.\)
Đó là phương trình chính tắc của elip cần tìm.
d) \(M(1;0)\) và \(N\left( {\frac{{\sqrt 3 }}{2};1} \right)\) thuộc elip \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{1}{{{a^2}}} + \frac{0}{{{b^2}}} = 1}\\
{\frac{3}{{4{a^2}}} + \frac{1}{{{b^2}}} = 1}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 1}\\
{\frac{3}{4} + \frac{1}{{{b^2}}} = 1}
\end{array}} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
a = 1\\
b = 2
\end{array} \right.\) \( \Rightarrow a < b\) suy ra không có phương trình chính tắc của elip trong hệ toạ độ đã cho.
e) Theo giả thiết \(\left\{ {\begin{array}{*{20}{l}}
{2c = 8}\\
{e = \frac{4}{5}}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{c = 4}\\
{\frac{c}{a} = \frac{4}{5}}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{c = 4}\\
{a = 5}
\end{array}} \right.\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{a^2} – {c^2} = 9}\\
{a = 5}
\end{array}} \right.\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{b^2} = 9}\\
{a = 5}
\end{array}} \right..\)
Thay vào \((1)\) ta có \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1.\)
Đó là phương trình chính tắc của elip cần tìm.
Bài toán 3. Chứng minh một số tính chất của elip.
Thí dụ 7: Trong mặt phẳng với hệ toạ độ Đề các vuông góc, cho elip \((E)\) có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0.\)
1) Chứng minh với mọi điểm \(M \in (E)\) ta đều có \(b \le OM \le a.\)
2) Gọi \({F_1}\) là tiêu điểm có toạ độ \(( – c;0).\) Tìm điểm \(M \in (E)\) sao cho \(M{F_1}\) ngắn nhất, dài nhất.
3) Gọi \(A\) là một giao điểm của đường thẳng \((\Delta ):y = kx\) với \((E).\) Tính \(OA\) theo \(a\), \(b\) và \(k.\)
4) Gọi \(A\), \(B\) là hai điểm thuộc \((E)\) sao cho \(OA \bot OB.\) Chứng minh: \(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\) có giá trị không đổi.
5) Gọi \((D)\) là đường thẳng \(AB\) nói ở câu 4, \(H\) là hình chiếu của \(O\) trên \((D).\) Chứng minh \((D)\) luôn tiếp xúc với một đường tròn cố định.
6) Gọi \(A’\), \(B’\) theo thứ tự là điểm đối xứng qua \(O\) lần lượt của \(A\), \(B.\) Tìm tứ giác \(ABB’A’\) có diện tích lớn nhất, nhỏ nhất.
1) Với mọi điểm \(M(x;y)\) ta có \(O{M^2} = {x^2} + {y^2}.\)
Do \(a > b \Rightarrow \frac{{{t^2}}}{{{a^2}}} \le \frac{{{t^2}}}{{{b^2}}}.\)
\(M \in (E) \Leftrightarrow \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)
Ta có: \(\frac{{O{M^2}}}{{{a^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{a^2}}}.\)
Suy ra \(\frac{{O{M^2}}}{{{a^2}}} \le \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \( \Leftrightarrow OM \le a.\)
Tương tự \(\frac{{O{M^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{b^2}}}\) \( \ge \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \( \Leftrightarrow OM \ge b.\)
2) Theo công thức bán kính qua tiêu điểm ta có \(M{F_1} = a + ex.\)
Mặt khác \(M \in (E)\) \( \Rightarrow – a \le x \le a\) \( \Rightarrow a + e( – a) \le M{F_1} \le a + ea.\)
\( \Leftrightarrow a – c \le M{F_1} \le a + c.\)
Vậy:
+ Giá trị bé nhất của \(M{F_1}\) là \(M{F_1} = a – c\) đạt được khi \(M \equiv {A_1}( – c;0).\)
+ Giá trị lớn nhất của \(M{F_1}\) là \(M{F_1} = a + c\) đạt được khi \(M \equiv {A_2}(c;0).\)
3) Toạ độ \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\:\:(1)}\\
{y = kx\:\:(2)}
\end{array}} \right..\)
Thay \((2)\) vào \((1)\) ta có: \({x^2}\left( {\frac{1}{{{a^2}}} + \frac{{{k^2}}}{{{b^2}}}} \right) = 1\) \( \Leftrightarrow {x^2} = \frac{{{a^2}{b^2}}}{{{b^2} + {k^2}{a^2}}}\) \((3).\)
Từ \((2)\) suy ra \({x^2} + {y^2} = \left( {1 + {k^2}} \right){x^2}\) \(\mathop \Leftrightarrow \limits^{(3)} {x^2} + {y^2} = \frac{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}{{{b^2} + {k^2}{a^2}}}\) \((4).\)
Hay \(OA = \frac{{ab\sqrt {1 + {k^2}} }}{{\sqrt {{b^2} + {k^2}{a^2}} }}\) \((5).\)
4) Từ \((5)\) suy ra \(\frac{1}{{O{A^2}}} = \frac{{{b^2} + {k^2}{a^2}}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}\) \((6).\)
\(OB \bot OA \Leftrightarrow B\) thuộc đường thẳng \(\left( {\Delta ‘} \right) \bot (\Delta )\) suy ra phương trình đường thẳng \(\left( {\Delta ‘} \right)\) qua \(O\), \(B\) là \(x = ky.\)
Toạ độ \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1}\\
{x = ky}
\end{array}} \right..\)
Tương tự như đối với \(A\) ta có \(\frac{1}{{O{B^2}}} = \frac{{{a^2} + {k^2}{b^2}}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}\) \((7).\)
Từ \((6)\), \((7)\) suy ra:
\(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\) \( = \frac{{{b^2} + {k^2}{a^2}}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}} + \frac{{{a^2} + {k^2}{b^2}}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}\) \( = \frac{{\left( {{a^2} + {b^2}} \right)\left( {1 + {k^2}} \right)}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}\) \( = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}.\)
Tóm lại \(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}\) (hằng số).
5) Trong tam giác \(AOB\) vuông tại \(O\), \(OH\) là đường cao ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}.\)
\( \Rightarrow \frac{1}{{O{H^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}\) \( \Leftrightarrow OH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}\) (hằng số).
Suy ra đường thẳng \((D)\) luôn tiếp xúc với đường tròn tâm \(O\), bán kính \(R = OH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}.\)
6) Rõ ràng tứ giác \(ABB’A’\) là hình thoi và có diện tích \(S = 2OA.OB.\)
Diện tích nhỏ nhất:
Áp dụng bất đẳng thức Côsi vào \((8)\) ta có:
\(\frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\) \( \ge \frac{2}{{OA.OB}} = \frac{4}{S}\) \( \Rightarrow S \ge \frac{{4{a^2}{b^2}}}{{{a^2} + {b^2}}}.\)
Dấu đẳng thức có khi và chỉ khi \(\frac{1}{{O{A^2}}} = \frac{1}{{O{B^2}}}\) \( \Leftrightarrow {b^2} + k{a^2} = {a^2} + k{b^2}.\)
\( \Leftrightarrow \left( {{a^2} – {b^2}} \right)\left( {{k^2} – 1} \right) = 0\) \( \Leftrightarrow {k^2} – 1 = 0\) \( \Leftrightarrow k = \pm 1\) \( \Leftrightarrow A\), \(B\) lần lượt thuộc các đường phân giác \(y = \pm x\) của góc hợp bởi các trục toạ độ.
Vậy giá trị nhỏ nhất của diện tích tứ giác \(ABB’A’\) là \(S = \frac{{4{a^2}{b^2}}}{{{a^2} + {b^2}}}.\)
Diện tích lớn nhất:
Từ \((6)\), \((7)\) suy ra \(\frac{1}{{OA}}.\frac{1}{{OB}}\) \( = \frac{{\sqrt {{b^2} + {k^2}{a^2}} }}{{ab\sqrt {1 + {k^2}} }}.\frac{{\sqrt {{a^2} + {k^2}{b^2}} }}{{ab\sqrt {1 + {k^2}} }}\) hay \(\frac{2}{S} \ge \frac{{\sqrt {\left( {{b^2} + {k^2}{a^2}} \right)\left( {{a^2} + {k^2}{b^2}} \right)} }}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}}\) \((9).\)
Theo bất đẳng thức Bunhiacopski:
\(\sqrt {\left( {{b^2} + {k^2}{a^2}} \right)\left( {{a^2} + {k^2}{b^2}} \right)} \) \( \ge ba + |k|a.|k|b\) \( = ab\left( {1 + {k^2}} \right).\)
Suy ra: \(\frac{2}{S} \ge \frac{{ab\left( {1 + {k^2}} \right)}}{{{a^2}{b^2}\left( {1 + {k^2}} \right)}} = \frac{1}{{ab}}\) \( \Rightarrow S \le 2ab.\)
Dấu đẳng thức có khi và chỉ khi \(\frac{{|k|a}}{b} = \frac{{|k|b}}{a}\) \( \Leftrightarrow |k|\left( {{a^2} – {b^2}} \right) = 0\) \( \Leftrightarrow k = 0.\)
\( \Leftrightarrow A\), \(B\), \(B’\), \(A’\) là bốn đỉnh của elip.
Vậy giá trị lớn nhất của diện tích tứ giác \(ABB’A’\) là \(S = 2ab.\)
Bài toán 4. Tập hợp điểm với elip.
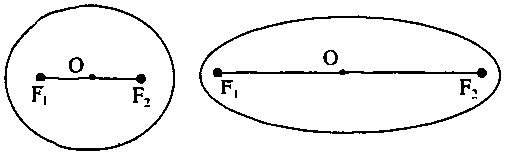
Thí dụ 8: Cho đường tròn \((O’)\) nằm trong đường tròn \((O).\) Tìm quỹ tích tâm \(I\) của các đường tròn tiếp xúc với cả hai đường tròn đã cho.
Gọi bán kính các đường tròn \((O)\), \((O’)\), \((I)\) lần lượt là \(R\), \(R’\) và \(r.\) Do \((O’)\) nằm trong \((O)\) nên \((I)\) tiếp xúc với cả hai đường tròn \((O)\) và \((O’)\) \( \Leftrightarrow (I)\) tiếp xúc trong với \((O)\) và tiếp xúc ngoài với \((O’).\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{IO = R – r}\\
{IO’ = R + r}
\end{array}} \right.\) \( \Rightarrow IO + IO’ = R + R’\) \((1).\)
Trường hợp 1: \(O \ne O’.\)
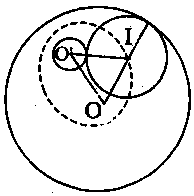
Từ \((1)\) suy ra tập hợp \(I\) là elip có các tiêu điểm là \(O\) và \(O’\), độ dài trục lớn là: \(2a = R + R’.\)
Trường hợp 2: \(O \equiv O’.\)
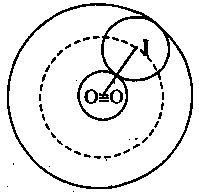
Khi đó \((1) \Leftrightarrow 2IO = R + R’\) \( \Leftrightarrow IO = \frac{{R + R’}}{2}\) \( \Rightarrow \) Tập hợp tâm \(I\) là đường tròn tâm \(O\), bán kính \(\frac{{R + R’}}{2}.\)
Khi đó \((1) \Leftrightarrow (I)\) tiếp xúc trong với \((O)\) và tiếp xúc ngoài với \((O’).\)
\( \Rightarrow \) Tập hợp tâm \(I\) là đường tròn tâm \(O\), bán kính \(\frac{{R + R’}}{2}.\)
Thí dụ 9: Trong mặt phẳng với hệ trục toạ độ vuông góc \(Oxy\), cho hai đường tròn đồng tâm \(O\), bán kính lần lượt là \({R_1} = a\), \({R_2} = b.\) Tia \(Ot\) cắt hai đường tròn theo thứ tự ở \(E\), \(F.\) Qua \(F\) kẻ đường thẳng \((\Delta )\) song song với trục \(Ox.\) Qua \(E\) kẻ đường thẳng \((\Delta ‘)\) song song với trục \(Oy.\) Gọi \(M\) là giao điểm của \((\Delta )\) và \((\Delta ‘).\) Tìm quỹ tích \(M\) khi \(Ot\) quay quanh \(O.\)
Xét bài toán trong hai trường hợp của tia \(Ot\) sau đây:
Trường hợp 1: Tia \(Ot\) thuộc nửa mặt phẳng có bờ là trục \(Ox\), chứa tia \(Oy.\)

Gọi \(K = (\Delta ) \cap Oy\), \(H = \left( {\Delta ‘} \right) \cap Ox\), \(\left( {{x_0};{y_0}} \right)\) là toạ độ điểm \(M\), \(\widehat {xOt} = \alpha \) với \({0^0} \le \alpha \le {180^0}.\)
Từ giả thiết suy ra \(OF=a\), \(OE=b\) và \(\left\{ {\begin{array}{*{20}{l}}
{{x_0} = \overline {OH} = OF\cos \alpha = a\cos \alpha }\\
{{y_0} = \overline {OK} = OE\sin \alpha = b\sin \alpha }
\end{array}} \right..\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{{x_0^2}}{{{a^2}}} = {{\cos }^2}\alpha }\\
{\frac{{y_0^2}}{{{b^2}}} = {{\sin }^2}\alpha }
\end{array}} \right.\) \( \Rightarrow \frac{{x_0^2}}{{{a^2}}} + \frac{{y_0^2}}{{{b^2}}} = {\cos ^2}\alpha + {\sin ^2}\alpha .\)
\( \Leftrightarrow \frac{{x_0^2}}{{{a^2}}} + \frac{{y_0^2}}{{{b^2}}} = 1.\)
Tập hợp các điểm \(M\) là nửa elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(y \ge 0.\)
Trường hợp 2:
Tia \(Ot\) thuộc nửa mặt phẳng có bờ là trục \(Ox\), chứa tia đối của tia \(Oy.\)
Gọi \(M’\) là điểm đối xứng của \(M\) qua \(Ox.\) Khi đó \(M’\) có tọa độ \(\left( {{x_0}; – {y_0}} \right).\)
Tương tự trên suy ra \(\frac{{x_0^2}}{{{a^2}}} + \frac{{{{\left( { – {y_0}} \right)}^2}}}{{{b^2}}} = 1\) \( \Leftrightarrow \frac{{x_0^2}}{{{a^2}}} + \frac{{y_0^2}}{{{b^2}}} = 1.\)
\( \Leftrightarrow \) Tập hợp các điểm \(M\) là nửa elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(y < 0.\)
Từ hai trường hợp trên kết luận: Tập hợp các điểm \(M\) phải tìm là đường elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)
Thí dụ 10. Cho hai đường tròn \(\left( {{C_1}} \right):{x^2} + {y^2} = 1\) và \(\left( {{C_2}} \right):{x^2} + {y^2} = 49.\) Gọi \(A\), \(B\) là các điểm theo thứ tự thuộc \(\left( {{C_1}} \right)\), \(\left( {{C_2}} \right)\) và \(I\) là trung điểm \(AB.\) Viết phương trình đường cong do \(I\) tạo thành khi \(A\), \(B\) thay đổi trên \(\left( {{C_1}} \right)\), \(\left( {{C_2}} \right)\) sao cho \(Ox\) luôn là phân giác của góc \(\widehat {AOB}.\)
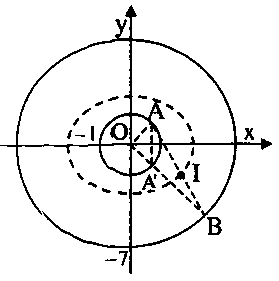
Gọi \({R_1}\), \({R_2}\) theo thứ tự là bán kính của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) có tâm tại \(O.\) Rõ ràng \({R_1} = 1\), \({R_2} = 7.\)
Gọi \(A’ = OA \cap \left( {{C_1}} \right)\) \( \Rightarrow \overrightarrow {OB} = \frac{{{R_2}}}{{{R_1}}}\overrightarrow {OA’} \) \( \Rightarrow \overrightarrow {OB} = 7\overrightarrow {OA’} .\)
Do \(Ox\) là phân giác của góc \(\widehat {AOB}\) \( \Rightarrow A’\) và \(A\) là hai điểm đối xứng nhau qua trục \(Ox.\) Do vậy gọi tọa độ của \(A\) là \(\left( {{x_0};{y_0}} \right)\) ta có \(A’\left( {{x_0}; – {y_0}} \right)\), \(B\left( {7{x_0}; – 7{y_0}} \right).\)
\(I\) là trung điểm \(AB\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_I} = \frac{{{x_A} + {x_B}}}{2}}\\
{{y_I} = \frac{{{y_A} + {y_B}}}{2}}
\end{array}} \right..\)
Hay \(\left\{ {\begin{array}{*{20}{l}}
{{x_I} = \frac{{{x_0} + 7{x_0}}}{2}}\\
{{y_I} = \frac{{{y_0} – 7{y_0}}}{2}}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_I} = 4{x_0}}\\
{{y_I} = – 3{y_0}}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{{x_I^2}}{{16}} = x_0^2}\\
{\frac{{y_I^2}}{9} = y_0^2}
\end{array}} \right..\)
\( \Rightarrow \frac{{x_I^2}}{{16}} + \frac{{y_I^2}}{9} = x_0^2 + y_0^2\) \((1).\)
\(B \in \left( {{C_1}} \right)\) \( \Leftrightarrow x_0^2 + y_0^2 = 1\) \((2).\)
Từ \((1)\) và \((2)\) suy ra: \(\frac{{x_I^2}}{{16}} + \frac{{y_I^2}}{9} = 1\) \( \Leftrightarrow I\) thuộc elip có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1.\)
Thí dụ 11: Cho đường cong \((E)\) có phương trình \(9{x^2} + 25{y^2} = 225\) \((1).\)
a) Đặt tên cho \((E).\) Nếu là elip hãy cho biết tiêu điểm, tâm sai của nó. Vẽ elip dựa trên hình chữ nhật cơ sở.
b) Viết phương trình đường thẳng \((\Delta )\) đi qua \(I(1;1)\) và cắt elip tại hai điểm \(E\), \(F\) sao cho \(I\) là trung điểm của \(EF.\)
c) Cho điểm \(A(-5;0).\) Gọi \(M\) là một điểm thuộc \((E)\), \(H\) là hình chiếu vuông góc của \(M\) trên trục \(Oy.\) Giả sử \(AH\) cắt \(OM\) tại \(P.\) Chứng minh khi \(M\) thay đổi trên \((E)\) thì \(P\) di chuyển trên đường cong cố định.
a) Viết lại \((1) \Leftrightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1.\) Đó là phương trình có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a = 5\), \(b = 3\) \( \Rightarrow (E)\) là đường elip.
Ta có \(c = \sqrt {{a^2} – {b^2}} \) \( = \sqrt {25 – 9} = 4\) \( \Rightarrow \) Tiêu điểm \({F_1}( – 4;0)\), \({F_2}(4;0)\), tâm sai \(e = \frac{c}{a} = \frac{4}{5}.\)
b) Để ý \(I \notin Ox \Rightarrow \) đường thẳng \(x=1\) không cắt elip \((E)\) tại hai điểm thoả mãn yêu cầu bài toán \((1).\)
Xét đường thẳng \((\Delta )\) qua \(I(1;1)\) có phương trình \(y = k(x – 1) + 1\) \((2).\)
Toạ độ các giao điểm \(E\), \(F\) của \((\Delta )\) và \((E)\) là nghiệm của hệ:
\(\left\{ {\begin{array}{*{20}{l}}
{9{x^2} + 25{y^2} = 225\:\:(3)}\\
{y = kx + 1 – k\:\:(4)}
\end{array}} \right..\)
Thế \((3)\) vào \((2)\) ta có \(9{x^2} + 25{(kx + 1 – k)^2} = 225.\)
\( \Leftrightarrow \left( {9 + 25{k^2}} \right){x^2} – 50k(k – 1)x\) \( + 25\left( {{k^2} – 2k – 8} \right) = 0\) \((5).\)
Để ý: thay toạ độ \(I\) vào vế trái phương trình \((1)\) có \(34 < 225\), suy ra \(I\) nằm trong đường elip, \( \Rightarrow (\Delta )\) luôn cắt \((E)\) tại hai điểm phân biệt \( \Leftrightarrow \) với mọi \(k\) phương trình \((5)\) có hai nghiệm phân biệt \({x_1}\), \({x_2}\), đó là hoành độ của \(E\) và \(F.\) Theo định lý Vi-ét ta có:
\({x_1} + {x_2} = \frac{{50k(k – 1)}}{{9 + 25{k^2}}}.\)
\(I\) là trung điểm \(EF\) \( \Leftrightarrow {x_1} + {x_2} = 2{x_I}\) hay \(\frac{{50k(k – 1)}}{{9 + 25{k^2}}} = 2.1\) \( \Leftrightarrow k = – \frac{9}{{25}}.\)
Thay vào \((2)\) ta có \(y = – \frac{9}{{25}}(x – 1) + 1\) \( \Leftrightarrow 9x + 25y – 34 = 0.\)
Từ \((1)\) và \((6)\) kết luận: \((6)\) là phương trình đường thẳng \((\Delta )\) mà ta cần tìm.
c) Với mọi điểm \(M\left( {{x_0};{y_0}} \right)\) ta có:

Phương trình đường thẳng \(OM\) là \(\frac{{x – 0}}{{{x_0} – 0}} = \frac{{y – 0}}{{{y_0} – 0}}\) \( \Leftrightarrow {y_0}x – {x_0}y = 0.\)
\(H\) là hình chiếu của \(M\) trên \(Oy\) \( \Leftrightarrow H\) có toạ độ \(H\left( {0;{y_0}} \right).\)
Phương trình đường thẳng \(AH\) là \(\frac{{x + 5}}{{0 + 5}} = \frac{{y – 0}}{{{y_0} – 0}}\) \( \Leftrightarrow {y_0}x – 5y + 5{y_0} = 0.\)
\(P = AH \cap OM\) \( \Leftrightarrow \) toạ độ \(P\) là nghiệm của hệ:
\(\left\{ {\begin{array}{*{20}{l}}
{{y_0}x – {x_0}y = 0}\\
{{y_0}x – 5y + 5{y_0} = 0}
\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x_0} = \frac{{5x}}{{x + 5}}}\\
{{y_0} = \frac{{5y}}{{x + 5}}}
\end{array}} \right..\)
\(M\left( {{x_0};{y_0}} \right)\) là một điểm thuộc \((E)\) \( \Leftrightarrow 9x_0^2 + 25y_0^2 = 225.\)
\( \Leftrightarrow 9{\left( {\frac{{5x}}{{x + 5}}} \right)^2} + 25{\left( {\frac{{5y}}{{x + 5}}} \right)^2} = 225.\)
\( \Leftrightarrow 9.25{x^2} + 25.25{y^2}\) \( = 9.25{(x + 5)^2}\) \( \Leftrightarrow {y^2} = \frac{{18}}{{25}}x + 9.\)
Vậy khi \(M\) thay đổi, \(P\) di chuyển trên đường cong cố định có phương trình \({y^2} = \frac{{18}}{{25}}x + 9.\)
Bài toán 5. Tương giao giữa elip và đường thẳng, elip và elip.
Thí dụ 12: Chứng minh định lý: Trong mặt phẳng toạ độ \(Oxy\), đường thẳng \((d):Ax + By + C = 0\) có điểm chung với elip \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) khi và chỉ khi \({A^2}{a^2} + {B^2}{b^2} \ge {C^2}.\)
\((d)\) và \((E)\) có điểm chung khi và chỉ khi hệ có nghiệm \((*)\left\{ {\begin{array}{*{20}{l}}
{Ax + By + C = 0\:\:(1)}\\
{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\:\:(2)}
\end{array}} \right..\)
Trường hợp 1: \(B = 0\) \((A \ne 0).\)
Khi đó \((1) \Leftrightarrow Ax + C = 0\) \( \Leftrightarrow x = – \frac{C}{A}\), thế vào \((2)\) có \(\frac{{{C^2}}}{{{A^2}{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \( \Leftrightarrow \frac{{{y^2}}}{{{b^2}}} = 1 – \frac{{{C^2}}}{{{A^2}{a^2}}}\) \((3).\)
Hệ \((*)\) có nghiệm \( \Leftrightarrow \) Phương trình \((3)\) có nghiệm \( \Leftrightarrow 1 – \frac{{{C^2}}}{{{A^2}{a^2}}} \ge 0.\)
\( \Leftrightarrow \frac{{{C^2}}}{{{A^2}{a^2}}} \le 1\) \( \Leftrightarrow {A^2}{a^2} \ge {C^2}\) hay (do \(B = 0\)) \({A^2}{a^2} + {B^2}{b^2} \ge {C^2}\) \((4).\)
Trường hợp 2: \(B \ne 0.\)
Khi đó \((1) \Leftrightarrow y = – \frac{{Ax + C}}{B}.\)
Thế vào \((2)\) có \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{{(Ax + C)}^2}}}{{{B^2}{b^2}}} = 1\) \( \Leftrightarrow {B^2}{b^2}{x^2} + {a^2}{(Ax + C)^2} = {a^2}{B^2}{b^2}.\)
\( \Leftrightarrow \left( {{A^2}{a^2} + {B^2}{b^2}} \right){x^2} + 2{a^2}ACx\) \( + {a^2}\left( {{C^2} – {B^2}{b^2}} \right) = 0\) \((5).\)
Hệ \((*)\) có nghiệm \( \Leftrightarrow \) phương trình \((5)\) có nghiệm \( \Leftrightarrow \Delta ‘ \ge 0.\)
\( \Leftrightarrow {a^4}{A^2}{C^2} – {a^2}\left( {{A^2}{a^2} + {B^2}{b^2}} \right)\left( {{C^2} – {B^2}{b^2}} \right) \ge 0.\)
\( \Leftrightarrow {B^2}{b^2}\left( {{A^2}{a^2} + {B^2}{b^2} – {C^2}} \right) \ge 0\) \( \Leftrightarrow {A^2}{a^2} + {B^2}{b^2} \ge {C^2}\) \((6).\)
Từ \((4)\) và \((6)\) ta có điều phải chứng minh.
Chú ý:
\({A^2}{a^2} + {B^2}{b^2} > {C^2}\) \( \Leftrightarrow (\Delta )\) và \((E)\) có hai điểm chung. Ta nói \((\Delta )\) cắt \((E).\)
\({A^2}{a^2} + {B^2}{b^2} = {C^2}\) \( \Leftrightarrow (\Delta )\) và \((E)\) có một điểm chung. Ta nói \((\Delta )\) và \((E)\) tiếp xúc với nhau.
Thí dụ 13: Xét vị trí tương đối giữa elip \((E):\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1\) với mỗi một đường thẳng sau đây:
\(\left( {{d_1}} \right):2x + y + 1 = 0.\)
\(\left( {{d_2}} \right):x + y – \sqrt {13} = 0.\)
\(({d_3}):x – 3y + 11 = 0.\)
Áp dụng chú ý ở thí dụ 12.
\(\left( {{d_1}} \right)\) cắt \((E)\) tại hai điểm phân biệt.
\(\left( {{d_2}} \right)\) và \((E)\) tiếp xúc với nhau.
\(\left( {{d_3}} \right)\) và \((E)\) không có điểm chung.
Thí dụ 14: Giả sử \(x\) và \(y\) liên hệ với nhau bởi hệ thức \(36{x^2} + 16{y^2} = 9.\) Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(U = y – 2x + 5.\)
Tập hợp giá trị của \(U\) là nghiệm của hệ:
\(\left\{ {\begin{array}{*{20}{l}}
{36{x^2} + 16{y^2} = 9}\\
{U = y – 2x + 5}
\end{array}} \right.\) \( \Leftrightarrow (*)\left\{ \begin{array}{l}
\frac{{{x^2}}}{{\frac{1}{4}}} + \frac{{{y^2}}}{{\frac{9}{{16}}}} = 1\\
2x – y + U – 5 = 0
\end{array} \right..\)
Xét elip \((E)\): \(\frac{{{x^2}}}{{\frac{1}{4}}} + \frac{{{y^2}}}{{\frac{9}{{16}}}} = 1\) và đường thẳng \((d):2x – y + U – 5 = 0.\)
Hệ \((*)\) có nghiệm \( \Leftrightarrow {a^2}{A^2} + {b^2}{B^2} \ge {C^2}\) \( \Leftrightarrow 4.\frac{1}{4} + 1.\frac{9}{{16}} \ge {(U – 5)^2}.\)
\( \Leftrightarrow {(U – 5)^2} \le \frac{{25}}{{16}}\) \( \Leftrightarrow |U – 5| \le \frac{5}{4}\) \( \Leftrightarrow – \frac{5}{4} \le U – 5 \le \frac{5}{4}\) \( \Leftrightarrow \frac{{15}}{4} \le U \le \frac{{25}}{4}.\)
Vậy \(\min U = \frac{{15}}{4}\) và \(\max U = \frac{{25}}{4}.\)
Thí dụ 15: Viết phương trình đường tròn đi qua các giao điểm của hai elip: \(\left( {{E_1}} \right):\frac{{{x^2}}}{{16}} + {y^2} = 1\) và \(\left( {{E_2}} \right):\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{16}} = 1.\)
Tọa độ giao điểm của \(\left( {{E_1}} \right)\) và \(\left( {{E_2}} \right)\) là nghiệm của hệ \((I)\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2}}}{{16}} + {y^2} = 1}\\
{\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{16}} = 1}
\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x^2} = \frac{{80}}{{21}}}\\
{{y^2} = \frac{{16}}{{21}}}
\end{array}} \right.\) \( \Leftrightarrow {x^2} + {y^2} = \frac{{32}}{7}.\)
Toạ độ các giao điểm của hai elip đã cho thoả mãn phương trình \({x^2} + {y^2} = \frac{{32}}{7}.\)
Bởi thế nên \({x^2} + {y^2} = \frac{{32}}{7}\) là phương trình đường tròn mà ta cần tìm.