Ví dụ minh họa:
Ví dụ 1: Cho hình bình hành \(ABCD\) tâm \(O.\) Đặt \(\overrightarrow {AO} = \overrightarrow a \), \(\overrightarrow {BO} = \overrightarrow b .\) Hãy biểu diễn các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {BC} \), \(\overrightarrow {CD} \) và \(\overrightarrow {DA} \) theo hai vectơ \(\overrightarrow a \), \(\overrightarrow b .\)
Ta có:
\(\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} = \vec a – \vec b.\)
\(\overrightarrow {BC} = \overrightarrow {BO} + \overrightarrow {OC} = \vec b + \vec a.\)
\(\overrightarrow {CD} = – \overrightarrow {AB} = \overrightarrow b – \overrightarrow a .\)
\(\overrightarrow {DA} = – \overrightarrow {BC} = – \overrightarrow b – \overrightarrow a .\)
Ví dụ 2: Cho tam giác \(ABC\) có trọng tâm là \(G\), \(H\) là điểm đối xứng của \(B\) qua \(G.\) Gọi \(M\) là trung điểm của \(BC.\) Đặt \(\overrightarrow {AB} = \overrightarrow b \), \(\overrightarrow {AC} = \overrightarrow c \). Biểu thị các vectơ \(\overrightarrow {AH} \), \(\overrightarrow {CH} \) và \(\overrightarrow {MH} \) theo \(\overrightarrow b \) và \(\overrightarrow c .\)
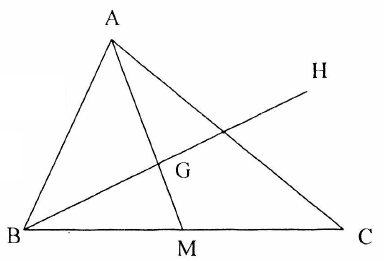
Ta có: \(\overrightarrow {AH} + \overrightarrow {AB} = 2\overrightarrow {AG} .\)
Suy ra: \(\overrightarrow {AH} = – \overrightarrow {AB} + \frac{4}{3}\overrightarrow {AM} \) \( = – \overrightarrow {AB} + \frac{2}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\) \( = – \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} .\)
Vậy: \(\overrightarrow {AH} = – \frac{1}{3}\overrightarrow b + \frac{2}{3}\overrightarrow c .\)
Tương tự:
\(\overrightarrow {CH} = \frac{2}{3}\overrightarrow {CA} – \frac{1}{3}\overrightarrow {CB} \) \( = – \frac{2}{3}\overrightarrow {AC} – \frac{1}{3}(\overrightarrow {AB} – \overrightarrow {AC} )\) \( = – \frac{1}{3}\overrightarrow {AB} – \frac{1}{3}\overrightarrow {AC} \) \( = – \frac{1}{3}(\overrightarrow {b} + \vec c).\)
\(\overrightarrow {MH} = \overrightarrow {MC} + \overrightarrow {CH} \) \( = \frac{1}{2}\overrightarrow {BC} – \frac{1}{3}(\vec b + \vec c)\) \( = \frac{1}{2}(\overrightarrow {AC} – \overrightarrow {AB} ) – \frac{1}{3}(\overrightarrow b + \overrightarrow c )\) \( = \frac{1}{2}(\overrightarrow c – \vec b) – \frac{1}{3}(\vec b + \vec c)\) \( = – \frac{5}{6}\vec b + \frac{1}{6}\overrightarrow c .\)
Ví dụ 3: Cho hình bình hành \(ABCD\) có \(M\), \(N\) là trung điểm của các cạnh \(DC\), \(DA.\) Đặt \(\overrightarrow {AM} = \vec a\), \(\overrightarrow {BN} = \vec b.\) Biểu diễn các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {BC} \), \(\overrightarrow {CD} \), \(\overrightarrow {DA} \), \(\overrightarrow {AC} \), \(\overrightarrow {BD} \) theo hai vectơ \(\overrightarrow a \), \(\overrightarrow b .\)
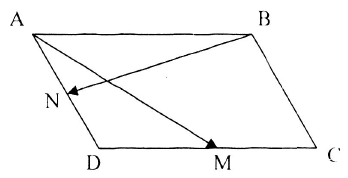
Ta có:
\(\overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {DM} \) \( = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} .\)
\(\overrightarrow {BN} = \overrightarrow {AN} – \overrightarrow {AB} \) \( = \frac{1}{2}\overrightarrow {AD} – \overrightarrow {AB} .\)
Từ đó: \(\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} = \vec a}\\
{\frac{1}{2}\overrightarrow {AD} – \overrightarrow {AB} = \vec b}
\end{array}} \right.\)
Giải hệ phương trình này ta được:
\(\overrightarrow {AB} = \frac{2}{3}\overrightarrow a – \frac{4}{5}\overrightarrow b .\)
\(\overrightarrow {AD} = \frac{4}{5}\overrightarrow a + \frac{2}{5}\overrightarrow b .\)
Như vậy:
\(\overrightarrow {AB} = \frac{2}{5}\overrightarrow a – \frac{4}{5}\overrightarrow b .\)
\(\overrightarrow {BC} = \overrightarrow {AD} = \frac{4}{5}\overrightarrow a + \frac{2}{5}\overrightarrow b .\)
\(\overrightarrow {CD} = – \overrightarrow {AB} = – \frac{2}{5}\overrightarrow a + \frac{4}{5}\overrightarrow b .\)
\(\overrightarrow {AD} = – \frac{4}{5}\overrightarrow a – \frac{2}{5}\overrightarrow b .\)
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = \frac{6}{5}\overrightarrow a – \frac{2}{5}\vec b.\)
\(\overrightarrow {BD} = \overrightarrow {AD} – \overrightarrow {AB} = \frac{2}{5}\vec a + \frac{6}{5}\vec b.\)
Ví dụ 4: Cho tam giác \(ABC.\) Gọi \(I\) là điểm trên cạnh \(BC\) sao cho \(2CI = 3BI\), gọi \(J\) là điểm trên phần kéo dài của cạnh \(BC\) sao cho \(5JB = 2JC.\)
a) Tính \(\overrightarrow {AI} \), \(\overrightarrow {AJ} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} .\)
b) Gọi \(G\) là trọng tâm tam giác \(ABC.\) Tính \(\overrightarrow {AG} \) theo \(\overrightarrow {AI} \) và \(\overrightarrow {AJ} .\)
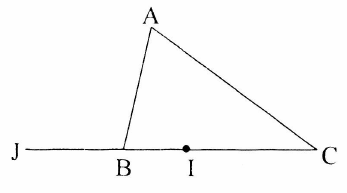
a) Vì \(I\) nằm trên cạnh \(BC\) và \(2CI = 3BI\) nên \(2\overrightarrow {CI} + 3\overrightarrow {BI} = \vec 0.\)
\( \Rightarrow 2(\overrightarrow {CA} + \overrightarrow {AI} ) + 3(\overrightarrow {BA} + \overrightarrow {AI} ) = \vec 0. \)
\( \Rightarrow 5\overrightarrow {AI} = 2\overrightarrow {AC} + 3\overrightarrow {AB} .\)
\( \Rightarrow \overrightarrow {AI} = \frac{2}{5}\overrightarrow {AC} + \frac{3}{5}\overrightarrow {AB} .\)
Vì \(J\) nằm trên phần kéo dài của cạnh \(BC\) và \(5JB = 2JC\) nên \(5\overrightarrow {JB} = 2\overrightarrow {JC} .\)
\( \Rightarrow 5(\overrightarrow {JA} + \overrightarrow {AB} ) = 2(\overrightarrow {JA} + \overrightarrow {AC} ).\)
\( \Rightarrow 3\overrightarrow {AJ} = 5\overrightarrow {AB} – 2\overrightarrow {AC} .\)
\( \Rightarrow \overrightarrow {AJ} = \frac{5}{3}\overrightarrow {AB} – \frac{2}{3}\overrightarrow {AC} .\)
b) Theo kết quả trên ta có:
\(\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} }\\
{\overrightarrow {AJ} = \frac{5}{3}\overrightarrow {AB} – \frac{2}{3}\overrightarrow {AC} }
\end{array}} \right.\)
Từ đó suy ra: \(\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AB} = \frac{5}{8}\overrightarrow {AI} + \frac{3}{8}\overrightarrow {AJ} }\\
{\overrightarrow {AC} = \frac{{25}}{{16}}\overrightarrow {AI} – \frac{9}{{16}}\overrightarrow {AJ} }
\end{array}} \right.\)
Ta lại có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \) (với \(M\) là trung điểm của \(BC\)) \( = \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\) \( = \frac{1}{3}\left( {\frac{5}{8}\overrightarrow {AI} + \frac{3}{8}\overrightarrow {AJ} + \frac{{25}}{{16}}\overrightarrow {AI} – \frac{9}{{16}}\overrightarrow {AJ} } \right)\) \( = \frac{{35}}{{48}}\overrightarrow {AI} – \frac{1}{{16}}\overrightarrow {AJ} .\)
Bài tập rèn luyện:
Bài toán 1: Cho tam giác \(ABC\), \(N\) là điểm sao cho \(\overrightarrow {CN} = \frac{1}{2}\overrightarrow {BC} .\) \(G\) là trọng tâm tam giác \(ABC.\) Biểu thị \(\overrightarrow {AC} \) theo \(\overrightarrow {AG} \) và \(\overrightarrow {AN} .\)
Bài toán 2: Cho tam giác \(ABC\) có \(D\), \(E\), \(F\) lần lượt là trung điểm của các cạnh \(BC\), \(CA\) và \(AB.\) Đặt \(\overrightarrow {BE} = \vec a\), \(\overrightarrow {CF} = \vec b.\) Biểu diễn các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {BC} \), \(\overrightarrow {CA} \) và \(\overrightarrow {AD} \) theo \(\overrightarrow a \) và \(\overrightarrow b .\)
Bài toán 3: Cho tam giác \(ABC\), \(I\) là điểm trên phần kéo dài của \(AB\) sao cho \(IA = 2IB\), \(J\) là điểm nằm trên cạnh \(AC\) sao cho \(3JA = 2JC.\) Biểu thị vectơ \(IJ\) theo \(\overrightarrow {AB} = \overrightarrow b \) và \(\overrightarrow {AC} = \vec c.\)
Bài toán 4: Cho hình bình hành \(ABCD\) tâm \(O\), \(I\) là trung điểm của \(BO\), \(G\) là trọng tâm tam giác \(OCD.\) Biểu thị các vectơ \(\overrightarrow {AI} \), \(\overrightarrow {BG} \) theo \(\overrightarrow {AB} = \vec a\) và \(\overrightarrow {AD} = \vec b.\)
Bài toán 5: Cho tam giác \(ABC.\) Gọi \(H\) là điểm đối xứng của trọng tâm \(G\) qua \(B.\)
a) Chứng minh rằng: \(\overrightarrow {HA} – 5\overrightarrow {HB} + \overrightarrow {HC} = \vec 0.\)
b) Đặt \(\overrightarrow {AG} = \vec a\), \(\overrightarrow {AH} = \vec b.\) Tính \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) theo \(\overrightarrow a \) và \(\overrightarrow b .\)
Bài toán 6: Cho lục giác đều \(ABCDEF.\) Đặt \(\overrightarrow u = \overrightarrow {AB} \), \(\overrightarrow v = \overrightarrow {AF} .\) Biểu thị các vectơ \(\overrightarrow {BC} \), \(\overrightarrow {CD} \), \(\overrightarrow {DE} \), \(\overrightarrow {EF} \), \(\overrightarrow {AC} \), \(\overrightarrow {AD} \), \(\overrightarrow {AE} \), \(\overrightarrow {BD} \), \(\overrightarrow {BE} \), \(\overrightarrow {BF} \), \(\overrightarrow {CE} \), \(\overrightarrow {CF} \), \(\overrightarrow {DF} \) theo \(\vec u\) và \(\overrightarrow v .\)
Bài toán 7: Cho tứ giác \(ABCD.\) Gọi \(M\), \(N\), \(E\), \(F\) là các điểm sao cho \(\overrightarrow {AM} = p\overrightarrow {AB} \), \(\overrightarrow {DN} = p\overrightarrow {DC} \), \(\overrightarrow {AE} = q\overrightarrow {AD} \), \(\overrightarrow {BF} = q\overrightarrow {BC} .\) \(MN\) cắt \(EF\) tại \(O.\) Tính \(\overrightarrow {EF} \) theo \(\overrightarrow {EM} \) và \(\overrightarrow {EN} .\)
Bài toán 8: Cho hình bình hành \(ABCD.\) Gọi \(M\), \(N\) là các điểm nằm trên đoạn \(AB\) và \(CD\) sao cho \(AM = \frac{1}{3}AB\), \(CN = \frac{1}{2}DC.\)
a) Tính \(\overrightarrow {AN} \) theo \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {AC} = \overrightarrow b .\)
b) Gọi \(G\) là trọng tâm tam giác \(MNB.\) Tính \(\overrightarrow {AG} \) theo \(\overrightarrow a \), \(\overrightarrow b .\)
c) Gọi \(I\), \(J\) lần lượt là các điểm xác định bởi \(\overrightarrow {BI} = m\overrightarrow {BC} \), \(\overrightarrow {AJ} = n\overrightarrow {AI} .\) Tính \(\overrightarrow {AI} \), \(\overrightarrow {AJ} \) theo \(\overrightarrow a \), \(\overrightarrow b \) và \(m\), \(n.\)
d) Xác định \(m\) để \(AI\) đi qua \(G.\)
e) Xác định \(m\), \(n\) để \(J\) là trọng tâm tam giác \(BMN.\)