A. PHƯƠNG PHÁP KHẢO SÁT SỰ BIẾN THIÊN CỦA HÀM SỐ
Cho hàm số \(f\) xác định trên \(K\).
• Hàm số \(y=f\left( x \right)\) đồng biến (tăng) trên \(K\) nếu \(\forall {{x}_{1}}\), \({{x}_{2}}\in K:\) \({{x}_{1}}<{{x}_{2}}\) \(\Rightarrow f({{x}_{1}})
Các phương pháp khảo sát sự biến thiên của hàm số:
• Cách 1: Cho hàm số \(y=f(x)\) xác định trên \(K\). Lấy \({{x}_{1}}\), \({{x}_{2}}\in K:\) \({{x}_{1}}<{{x}_{2}}\), đặt \(T=f({{x}_{2}})-f({{x}_{1}})\), khi đó:
+ Hàm số đồng biến trên \(K\) \(\Leftrightarrow T>0\).
+ Hàm số nghịch biến trên \(K\) \(\Leftrightarrow T<0\).
• Cách 2: Cho hàm số \(y=f(x)\) xác định trên \(K\). Lấy \({{x}_{1}}\), \({{x}_{2}}\in K:\) \({{x}_{1}}\ne {{x}_{2}}\), đặt \(T=\frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}\), khi đó:
+ Hàm số đồng biến trên \(K\) \(\Leftrightarrow T>0\).
+ Hàm số nghịch biến trên \(K\) \(\Leftrightarrow T<0\).
B. VÍ DỤ MINH HỌA
Ví dụ 1. Khảo sát sự biến thiên của hàm số sau trên khoảng \(\left( 1;+\infty \right).\)
a) \(y=\frac{3}{x-1}.\)
b) \(y=x+\frac{1}{x}.\)
a) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \left( 1;+\infty \right)\), \({{x}_{1}}\ne {{x}_{2}}\) ta có \(f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\frac{3}{{{x}_{2}}-1}-\frac{3}{{{x}_{1}}-1}\) \(=\frac{3\left( {{x}_{1}}-{{x}_{2}} \right)}{\left( {{x}_{2}}-1 \right)\left( {{x}_{1}}-1 \right)}.\)
Suy ra \(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=-\frac{3}{\left( {{x}_{2}}-1 \right)\left( {{x}_{1}}-1 \right)}.\)
Vì \({{x}_{1}}>1\), \({{x}_{2}}>1\) \(\Rightarrow \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}<0\) nên hàm số \(y=\frac{3}{x-1}\) nghịch biến trên khoảng \(\left( 1;+\infty \right).\)
b) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \left( 1;+\infty \right)\), \({{x}_{1}}\ne {{x}_{2}}\) ta có: \(f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\left( {{x}_{2}}+\frac{1}{{{x}_{2}}} \right)-\left( {{x}_{1}}+\frac{1}{{{x}_{1}}} \right)\) \(=\left( {{x}_{2}}-{{x}_{1}} \right)\left( 1-\frac{1}{{{x}_{1}}{{x}_{2}}} \right).\)
Suy ra \(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=1-\frac{1}{{{x}_{1}}{{x}_{2}}}.\)
Vì \({{x}_{1}}>1\), \({{x}_{2}}>1\) \(\Rightarrow \frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}>0\) nên hàm số \(y=x+\frac{1}{x}\) đồng biến trên khoảng \(\left( 1;+\infty \right).\)
Ví dụ 2. Cho hàm số \(y={{x}^{2}}-4.\)
a) Khảo sát sự biến thiên của hàm số trên \(\left( -\infty ;0 \right)\) và trên \(\left( 0;+\infty \right).\)
b) Lập bảng biến thiên của hàm số trên \(\left[ -1;3 \right]\), từ đó xác định giá trị lớn nhất, nhỏ nhất của hàm số trên \(\left[ -1;3 \right].\)
Tập xác định của hàm số: \(D=R.\)
a) \(\forall {{x}_{1}}\), \({{x}_{2}}\in \mathbb{R}\), \({{x}_{1}}<{{x}_{2}}\) \(\Rightarrow {{x}_{2}}-{{x}_{1}}>0.\)
Ta có \(T=f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\left( x_{2}^{2}-4 \right)-\left( x_{1}^{2}-4 \right)\) \(=x_{2}^{2}-x_{1}^{2}\) \(=\left( {{x}_{2}}-{{x}_{1}} \right).\left( {{x}_{1}}+{{x}_{2}} \right).\)
Nếu \({{x}_{1}}\), \({{x}_{2}}\in \left( -\infty ;0 \right)\) \(\Rightarrow T<0\). Vậy hàm số \(y=f\left( x \right)\) nghịch biến trên \(\left( -\infty ;0 \right).\)
Nếu \({{x}_{1}}\), \({{x}_{2}}\in \left( 0;+\infty \right)\) \(\Rightarrow T>0\). Vậy hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( 0;+\infty \right).\)
b) Bảng biến thiên của hàm số \(y={{x}^{2}}-4\) trên \(\left[ -1;3 \right]:\)
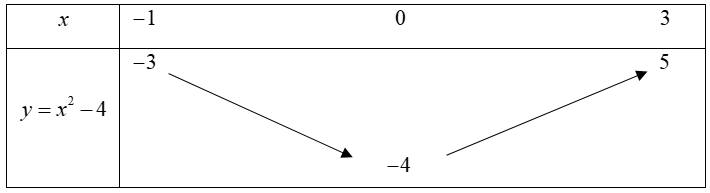
Dựa vào bảng biến thiên, ta có: \(\mathop {\max}\limits_{\left[ { – 1;3} \right]} y = 5\) khi và chỉ khi \(x=3\), \(\mathop {\min }\limits_{\left[ { – 1;3} \right]} y = – 4\) khi và chỉ khi \(x=0.\)
Ví dụ 3. Khảo sát sự biến thiên của hàm số \(y=\sqrt{4x+5}+\sqrt{x-1}\) trên tập xác định của nó. Áp dụng giải phương trình:
a) \(\sqrt{4x+5}+\sqrt{x-1}=3.\)
b) \(\sqrt{4x+5}+\sqrt{x-1}=\sqrt{4{{x}^{2}}+9}+x.\)
Điều kiện xác định: \(\left\{ \begin{matrix}
4x+5\ge 0 \\
x-1\ge 0 \\
\end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix}
x\ge -\frac{5}{4} \\
x\ge 1 \\
\end{matrix} \right.\) \(\Leftrightarrow x\ge 1.\)
Suy ra tập xác định của hàm số: \(\text{D}=\left[ 1;+\infty \right).\)
Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \left[ 1;+\infty \right)\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(f\left( {{x_2}} \right) – f\left( {{x_1}} \right)\) \( = \sqrt {4{x_2} + 5} + \sqrt {{x_2} – 1} \) \( – \sqrt {4{x_1} + 5} – \sqrt {{x_1} – 1} \) \( = \frac{{4\left( {{x_2} – {x_1}} \right)}}{{\sqrt {4{x_2} + 5} + \sqrt {4{x_1} + 5} }}\) \( + \frac{{{x_2} – {x_1}}}{{\sqrt {{x_2} – 1} + \sqrt {{x_1} – 1} }}\) \( = \left( {{x_2} – {x_1}} \right)\)\(\left( {\frac{4}{{\sqrt {4{x_2} + 5} + \sqrt {4{x_1} + 5} }} + \frac{1}{{\sqrt {{x_2} – 1} + \sqrt {{x_1} – 1} }}} \right).\)
Suy ra \(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=\frac{4}{\sqrt{4{{x}_{2}}+5}+\sqrt{4{{x}_{1}}+5}}\) \(+\frac{1}{\sqrt{{{x}_{2}}-1}+\sqrt{{{x}_{1}}-1}}>0.\)
Nên hàm số \(y=\sqrt{4x+5}+\sqrt{x-1}\) đồng biến trên khoảng \(\left[ 1;+\infty \right).\)
a) Vì hàm số đã cho đồng biến trên \(\left[ 1;+\infty \right)\) nên:
+ Nếu \(x>1\) \(\Rightarrow f\left( x \right)>f\left( 1 \right)\) hay \(\sqrt{4x+5}+\sqrt{x-1}>3\), suy ra phương trình \(\sqrt{4x+5}+\sqrt{x-1}=3\) vô nghiệm.
+ Nếu \(x<1\) \(\Rightarrow f\left( x \right)
Vậy phương trình có nghiệm duy nhất \(x=1.\)
b) Điều kiện xác định: \(x\ge 1.\)
Đặt \({{x}^{2}}+1=t\), \(t\ge 1\) \(\Rightarrow {{x}^{2}}=t-1\) phương trình trở thành: \(\sqrt{4x+5}+\sqrt{x-1}=\sqrt{4t+5}+\sqrt{t-1}\) \(\Leftrightarrow f\left( x \right)=f\left( t \right).\)
+ Nếu \(x>t\) \(\Rightarrow f\left( x \right)>f\left( t \right)\) hay \(\sqrt{4x+5}+\sqrt{x-1}>\sqrt{4t+5}+\sqrt{t-1}\), suy ra phương trình đã cho vô nghiệm.
+ Nếu \(x
Vậy phương trình đã cho vô nghiệm.
Nhận xét:
+ Hàm số \(y=f\left( x \right)\) đồng biến (hoặc nghịch biến) thì phương trình \(f\left( x \right)=0\) có tối đa một nghiệm.
+ Nếu hàm số \(y=f(x)\) đồng biến (nghịch biến) trên \(D\) thì \(f(x)>f(y)\) \(\Leftrightarrow x>y\) \((x
1. Đề bài
Bài toán 1. Khảo sát sự biến thiên của các hàm số sau:
a) \(y=4-3x.\)
b) \(y={{x}^{2}}+4x-5.\)
c) \(y=\frac{2}{x-2}\) trên \(\left( -\infty ;2 \right)\) và trên \(\left( 2;+\infty \right).\)
d) \(y=\frac{x}{x-1}\) trên \(\left( -\infty ;1 \right).\)
Bài toán 2. Chứng minh rằng hàm số \(y={{x}^{3}}+x\) đồng biến trên \(\mathbb{R}.\) Áp dụng giải phương trình sau \({{x}^{3}}-x=\sqrt[3]{2x+1}+1.\)
Bài toán 3. Cho hàm số \(y=\sqrt{x-1}+{{x}^{2}}-2x.\)
a) Khảo sát sự biến thiên của hàm số đã cho trên \(\left[ 1;+\infty \right).\)
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn \(\left[ 2;5 \right].\)
2. Hướng dẫn giải và đáp số
Bài toán 1.
a) Hàm số đồng biến trên \(\left( -\infty ;\frac{4}{3} \right)\) và nghịch biến trên khoảng \(\left( \frac{4}{3};+\infty \right).\)
b) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \mathbb{R}\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(K=\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=\frac{\left( x_{2}^{2}+4{{x}_{2}}-5 \right)-\left( x_{1}^{2}+4{{x}_{1}}-5 \right)}{{{x}_{2}}-{{x}_{1}}}\) \(={{x}_{1}}+{{x}_{2}}+4.\)
+ Với \({{x}_{1}}\), \({{x}_{2}}\in \left( -\infty ;-2 \right)\) \(\Rightarrow K<0\), suy ra hàm số nghịch biến trên \(\left( -\infty ;-2 \right).\)
+ Với \({{x}_{1}}\), \({{x}_{2}}\in \left( -2;+\infty \right)\) \(\Rightarrow K>0\), suy ra hàm số đồng biến trên \(\left( -2;+\infty \right).\)
c) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \mathbb{R}\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\frac{2}{{{x}_{2}}-2}-\frac{2}{{{x}_{1}}-2}\) \(=\frac{2\left( {{x}_{1}}-{{x}_{2}} \right)}{\left( {{x}_{2}}-2 \right)\left( {{x}_{1}}-2 \right)}\) \(\Rightarrow K=-\frac{2}{\left( {{x}_{2}}-2 \right)\left( {{x}_{1}}-2 \right)}.\)
+ Với \({{x}_{1}}\), \({{x}_{2}}\in \left( -\infty ;2 \right)\) \(\Rightarrow K<0\), do đó hàm số nghịch biến trên \(\left( -\infty ;2 \right).\)
+ Với \({{x}_{1}}\), \({{x}_{2}}\in \left( 2;+\infty \right)\) \(\Rightarrow K<0\), do đó hàm số nghịch biến trên \(\left( 2;+\infty \right).\)
d) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \left( -\infty ;1 \right)\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\frac{{{x}_{2}}}{{{x}_{2}}-1}-\frac{{{x}_{1}}}{{{x}_{1}}-1}\) \(=\frac{{{x}_{1}}-{{x}_{2}}}{\left( {{x}_{2}}-1 \right)\left( {{x}_{1}}-1 \right)}.\)
Suy ra \(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=\frac{-1}{\left( {{x}_{2}}-1 \right)\left( {{x}_{1}}-1 \right)}<0.\)
Vậy hàm số nghịch biến trên \(\left( -\infty ;-1 \right).\)
Bài toán 2.
Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \mathbb{R}\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=\frac{\left( x_{2}^{3}+{{x}_{2}} \right)-\left( x_{1}^{3}+{{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=x_{2}^{2}+x_{1}^{2}+{{x}_{2}}{{x}_{1}}+1>0.\)
Suy ra hàm số đã cho đồng biến trên \(\mathbb{R}.\)
Ta có \({{x}^{3}}-x=\sqrt[3]{2x+1}+1\) \(\Leftrightarrow {{x}^{3}}+x=2x+1+\sqrt[3]{2x+1}.\)
Đặt \(\sqrt[3]{2x+1}=y\), phương trình trở thành \({{x}^{3}}+x={{y}^{3}}+y.\)
Do hàm số \(f\left( x \right)={{x}^{3}}+x\) đồng biến trên \(\mathbb{R}\) nên: \(x=y\) \(\Rightarrow \sqrt[3]{2x+1}=x\) \(\Leftrightarrow {{x}^{3}}-2x-1=0\) \(\Leftrightarrow \left[ \begin{matrix}
x=-1 \\
x=\frac{1\pm \sqrt{5}}{2} \\
\end{matrix} \right.\)
Bài toán 3.
a) Với mọi \({{x}_{1}}\), \({{x}_{2}}\in \left[ 1;+\infty \right)\), \({{x}_{1}}\ne {{x}_{2}}\) ta có:
\(f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\) \(=\left( \sqrt{{{x}_{2}}-1}+x_{2}^{2}-2{{x}_{2}} \right)\) \(-\left( \sqrt{{{x}_{1}}-1}+x_{1}^{2}-2{{x}_{1}} \right)\) \(=\frac{{{x}_{2}}-{{x}_{1}}}{\sqrt{{{x}_{2}}-1}+\sqrt{{{x}_{1}}-1}}\) \(+\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{2}}+{{x}_{1}}-2 \right).\)
Suy ra \(\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\) \(=\frac{1}{\sqrt{{{x}_{2}}-1}+\sqrt{{{x}_{1}}-1}}+{{x}_{2}}+{{x}_{1}}-2>0.\)
Do đó hàm số đã cho đồng biến trên \(\left[ 1;+\infty \right).\)
b) Hàm số đã cho đồng biến trên \(\left[ 1;+\infty \right)\) nên nó đồng biến trên \(\left[ 2;5 \right].\)
Vậy \(\underset{\left[ 2;5 \right]}{\mathop{\max y}} =y\left( 5 \right)=17\) \(\Leftrightarrow x=5\), \(\underset{\left[ 2;5 \right]}{\mathop{\min y}} =y\left( 2 \right)=1\) \(\Leftrightarrow x=2.\)